Thermal Radiation Effects on Entropy Generation in Porous Media with Casson Fluid via FEM Insights

Introduction

In porous media, natural convection involving non-Newtonian Casson fluids has attracted considerable interest due to its relevance in various industrial and environmental applications. Analyzing entropy generation in such systems is essential for understanding the irreversibilities and inefficiencies inherent in heat transfer processes. In this regard, the Finite Element Method (FEM) stands out as a potent numerical tool for in-depth analysis. This study focuses on entropy generation within the framework of natural convection in a porous medium using Casson fluid, emphasizing the significance of FEM as a computational approach to explore the complex interactions of fluid dynamics and heat transfer. By investigating entropy generation, researchers can derive critical insights that enhance energy transfer efficiency and overall performance in natural convection processes, which are crucial for a range of engineering and environmental applications [1, 2].

Casson fluids, known for their shear-thinning properties, return to their original state upon the removal of applied shear stress, classifying them as viscoelastic. This rheological model has found successful applications in various sectors, such as food processing, pharmaceuticals, cosmetics, and oil drilling, to better understand and predict the flow behavior of non-Newtonian materials. However, its application in natural convection and entropy generation within the Darcy-Forchheimer model remains relatively unexplored. Pop et al. [3] conducted a pioneering study investigating heat transfer systems of Casson fluid in a square enclosure under thermal gradients, providing insights into the convective heat transfer characteristics that can be leveraged to optimize systems involving Casson fluids subjected to thermal radiation and viscous dissipation effects. Furthermore, Hamid et al. [4] examined fluid flow phenomena within a trapezoidal enclosure containing a Casson fluid, while Aneja et al. [5] studied buoyancyinduced convective phenomena involving a heated porous hollow with Casson fluid. The findings from these investigations have significant implications for various engineering applications involving non-Newtonian fluids, such as energy systems, environmental engineering, and materials processing. Aghighi et al. [6] explored double-diffusive natural convection, highlighting the concurrent transport of heat and mass due to density differences and revealing the effects of double diffusion and Casson fluid behavior on flow and temperature distributions. Additionally, Shah et al. [7] analyzed the behavior of Casson fluids in a curved corrugated cavity, considering the influences of convective heat and mass transport.

Entropy generation, being an irreversible natural process, is present in all heat transport processes as described by the second law of thermodynamics. It serves as a qualitative representation of energy loss in many systems, quantifying the rate at which useful energy transforms into less useful forms, such as thermal energy dissipation. By examining entropy generation, valuable insights can be obtained regarding the efficiency and performance of convective heat transfer systems. Moreover, studying entropy creation in natural convection sheds light on the irreversibilities and energy losses associated with these processes. Gireesha et al. [8] evaluated entropy generation and heat transfer in the flow of Casson fluids within an inclined porous microchannel, looking at the effects of viscous and Joule heating. Kotha et al. [9] explored the behavior of Casson fluid on a convectively heated surface and examined its entropy generation characteristics, considering viscous dissipation resulting from the fluid's internal friction that converts mechanical energy into heat. Sohail et al. [10] further investigated Casson fluid dynamics and its associated entropy generation characteristics. Alzahrani et al. [11] studied the posture of Casson fluids in an enclosure while analyzing convection and thermal radiation characteristics, focusing on entropy generation as a measure of irreversibility and energy dissipation. Hossain et al. [12] concentrated on Casson fluids in a staggered cavity and studied entropy generation in the context of double diffusive free convection, considering magnetic effects that can influence heat transfer and entropy generation, representing irreversible energy loss within the system. In porous media, where fluid flows through a solid matrix characterized by interconnected voids, the Brinkman-Forchheimer model is frequently utilized to describe fluid flow behavior. This model incorporates both viscous and inertial effects and has been shown to effectively capture the flow characteristics within such systems.

The Darcy-Forchheimer model is particularly useful for analyzing natural convection in porous media, where the convective flow is largely influenced by the porous structure. It is essential to note that many practical fluids exhibit non-Newtonian behavior, diverging from the classical assumption of Newtonian viscosity. Non-Newtonian fluids demonstrate complex flow characteristics due to phenomena such as shear-thinning, shear-thickening, yield stress, and viscoelasticity. Seth et al. [13] examined the behavior of Casson fluid in a rotating system within a porous enclosure, considering the impact of Darcy-Forchheimer porous media. They observed interactions between fluid rotation and porosity that affected the flow characteristics. Qawasmeh et al. [14] investigated buoyancy-driven convective heat transfer of Casson fluid in Darcy-Forchheimer porous media. Additionally, Farooq et al. [15] explored the flow of Casson fluid within an enclosure using a non-Darcy model. Zhang et al. [16] studied the flow of DarcyForchheimer Casson fluid over an extending sheet. Likewise, Li et al. [17] analyzed the effects of activation energy on DarcyForchheimer flow of a Casson fluid through a channel. The finite element method (FEM) will be employed as a numerical tool to solve the governing equations, accounting for the nonNewtonian characteristics of the Casson fluid. This study aims to enhance understanding of how properties of the Casson fluid, such as yield stress and flow behavior index, affect convective flow patterns, heat transfer features, and entropy generation rates.

Finite element analysis (FEA) divides the domain into smaller finite elements to compare solutions. Over the past few decades, researchers have harnessed FEM to analyze fluid flow interactions in complex scenarios. For instance, Raju et al. [18] used FEM to explore the free convective flow of Casson fluid over a vertically inclined plate, demonstrating the plate's angle relative to the horizontal axis. Reddy et al. [19] investigated the dissipation effects on fluid flow behavior, which can significantly influence the fluid's temperature distribution. Consequently, Goud et al. [20] examined the flow of Casson fluid in a vertically oscillating plate situated in a porous enclosure, where the oscillatory motion introduces time-dependent behavior into the flow. Rehman et al. [21] applied finite element analysis as a numerical technique to investigate the thermal behavior of a Casson liquid suspension. Shahzad et al. [22] explored Casson fluid flow in a bifurcated channel, which divides into two or more branches, and includes a stenosis, characterized by a constriction in the channel geometry.

Natural convection occurs as a heat transfer process induced by density differences in a fluid resulting from temperature gradients. This phenomenon plays a vital role in various engineering and environmental systems. A thorough understanding of buoyancydriven convection is essential for optimizing heat transfer and energy efficiency across numerous applications, including geothermal systems, solar collectors, building ventilation, and electronic cooling. Recent noteworthy research has zeroed in on natural convection, as evidenced by substantial contributions in the field of buoyancy-driven convection. Khan et al. [23] investigated the effects of several factors on natural convection using Casson fluid flow over a porous plate. Alwawi et al. [24] focused on the natural convection of a Casson nanofluid within an enclosure. Following this, Devi et al. [25] studied the natural convection of viscoelastic Casson fluid flows. Anwar et al. [26] explored the behavior of Casson fluid under variable wall conditions, taking into account thermal radiative flux and heat injection processes alongside natural convection.

Expanding the scope of the investigation to encompass additional non-Newtonian fluids, such as power-law and viscoplastic fluids, can significantly broaden the findings' applicability by exploring the unique rheological behaviors exhibited by these fluids. Power-law fluids are characterized by shear-thinning or shear-thickening properties and are prevalent in industries like food processing, polymer manufacturing, and biological systems. Viscoplastic fluids are distinguished by their yield stress, which separates solid-like behavior from flow regimes; these fluids are crucial in applications such as mining slurries, cement flow, and enhanced oil recovery. By analyzing entropy generation and heat transfer characteristics, researchers can assess how factors like flow indices, yield stress, and thermal properties influence system efficiency and irreversibilities. This comprehensive exploration could result in optimized designs for processes such as thermal management systems, chemical reactors, and heat exchangers, bolstered by sophisticated numerical modeling and experimental data, thereby deepening the understanding of non-Newtonian fluid dynamics across diverse practical applications [27-35].

This study aims to enhance the understanding of thermodynamic efficiency within convective heat transfer systems involving Casson fluids. The results from this research can inform the design and optimization of various engineering and environmental systems, promoting improved energy efficiency and sustainability alongside entropy generation. The research has enhanced existing models by revising the Darcy-Forchheimer model in the momentum equation. Additionally, the radiation term has been integrated into the energy and entropy equations using the Roseland approximation. The study also examined the effects of key dimensionless parameters.

Mathematical Formulation and Physical Representation

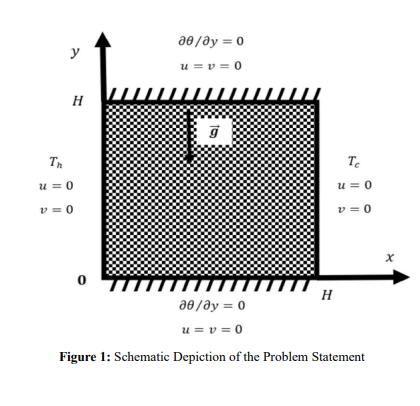
The present study investigates the behavior of buoyant convective unsteady laminar flow within a square two-dimensional cavity of length (H). This cavity is filled with a Casson liquid, which flows through a porous medium as illustrated in Fig. (1). In this analysis, the left wall of the cavity maintains a constant higher temperature (T_h ), while the right wall maintains a constant lower temperature (T_c ). The horizontal walls of the enclosure are treated as adiabatic. Gravity is incorporated into the y-momentum equation, and thermal radiation is taken into account in the energy equation. In the buoyancy equation, the thermal properties of the liquid are considered constant, with the exception of the density term, which adheres to the Boussinesq approximation, where the density of the liquid is related to its thermal expansion coefficient. The Casson fluid rheological model is obtained as Eq. (1)

Governing Equations

The dimensionless equations for this problem are given below

Boundary Condition

For the criteria given for the initial and boundary, the dimensionless variables are [29,30,31,35].

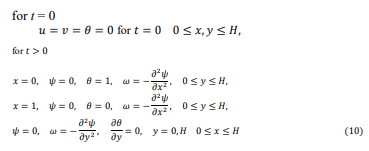
Entropy Generation

Entropy generation is a fundamental aspect of thermodynamics, and it is crucial in finding the effectiveness and irreversibility of processes. In practical applications, minimizing entropy generation is desirable to improve efficiency and reduce energy losses. Heat transfer happens from the hotter body to the colder body when there is a temperature differential between the two bodies. This heat transfer process leads to an increase in entropy. The magnitude of entropy creation due to heat transfer depends on the temperature difference, the nature of the heat transfer process (conduction, convection, or radiation), and the efficiency of the process. Friction between surfaces results in energy dissipation and heat generation. This energy dissipation contributes to an increase in entropy. When two surfaces slide or rub against each other, the frictional forces convert mechanical energy into heat. The magnitude of entropy creation due to friction depends on the frictional forces, the relative velocity of the surfaces, and the nature of the frictional contact. The total entropy creation in a system or a process is the sum of entropy contributions from all the sources involved. If there are multiple heat transfer processes and frictional interactions occurring simultaneously, the creation of overall entropy is the sum of entropy generated due to each individual source. Mathematically, Eq. (11) to Eq. (13) shows entropy lead by heat, friction, and overall entropy expressed by: [32,33,34].

Numerical Simulation and Validation of Code

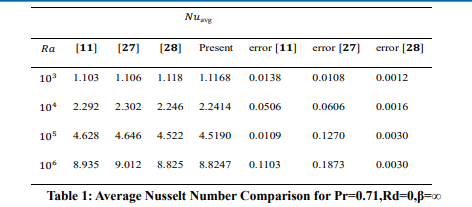
For this computation, we employed the finite element method as our numerical scheme. The domain was discretized into smaller, geometrically simple sections called finite elements to model the behavior of the Casson fluid and derive valuable insights. We utilized quadrilaterals within each element to represent the behavior of unknown quantities of interest. These quadrilaterals enable us to estimate the solution using a finite number of nodal points, leading to more efficient calculations. The computed average Nusselt numbers were compared against available experimental data and established benchmark solutions from Alzahrani et al. [11], Fusegi et al. [27], and Ho et al. [28] for various Rayleigh numbers (Ra =103 , 104 , 105 , 106 ), as shown in Table 1. This comparison included a comprehensive analysis of deviations, evaluating the agreement between the computational results and reference works. The outcomes for the average Nusselt number showed good alignment with existing findings, exhibiting minimal error. The errors were determined by comparing the current work to the existing literature [11,27,28].

error = Present - existing

Results and Discussion

The result of this investigation is presented in this section. The parameters under study includes Rayleigh number (103 ≤ Ra ≤ 106 ), Eckert number (10-6 ≤ Ec ≤ 10-4 ), Forchheimer number (0 ≤ Γ ≤ 1), inverse Darcy (0 ≤ γ ≤ 1), radiation (0 ≤ Rd ≤ 10), Prandtl number (Pr = 0.7,1.0,7.0,10) and Casson fluid parameters (0.001 ≤ β ≤ 1). Figure (2 - 10) shows the effects of dimensionless parameters on streamlines, isotherms, isolines of entropy, velocity, Nusselt number, and total entropy.

Effects of Rayleigh Number

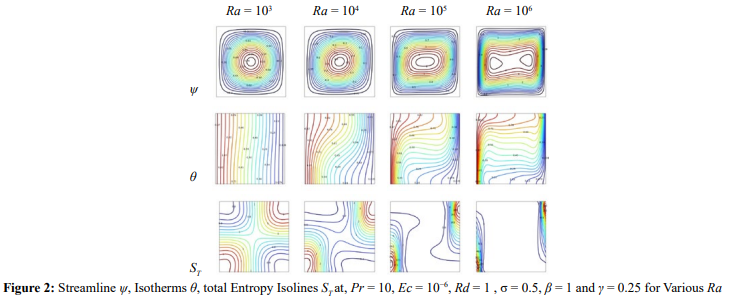
Figure 2 illustrates the streamline patterns, isotherms, and total entropy isolines for various Rayleigh numbers, while holding certain parameters constant Pr = 10, Ec = 10^-6, Rd = 1, σ = 0.5, β = 1 and γ = 0.25. The Rayleigh number plays a significant role in determining the flow patterns and the arrangement of streamlines in a fluid. At low Rayleigh numbers (Ra = 10³ ), the flow is generally steady and laminar, with streamlines tracing relatively smooth trajectories. As the Rayleigh number increases from 10³ to 10⁶ , the isotherms transition from a smooth, circular configuration indicative of a single convective core regime to patterns that display unsteady, intricate, and chaotic behavior, indicative of a double convective core regime. Figure 2 shows a near thermal stratification at a specified Rayleigh number Ra = 10³ . As the Rayleigh number rises, the isotherms exhibit greater temperature variations and more distinct gradients, which is attributed to intensified convective heat transfer in the context of natural convection. The Rayleigh number also influences the entropy distribution within the fluid indirectly by affecting temperature distribution. As the Rayleigh number increases from 10³ to 10⁶ , entropy isolines become more concentrated along the walls of the cavity, as depicted in Figure 2 [32,33].

Figure 3 presents the velocity, Nusselt number, and total entropy. The Rayleigh number significantly influences the flow velocity distribution in a fluid system. In the context of natural convection, as the Rayleigh number rises, buoyancy-driven flow becomes increasingly dominant over viscous forces. Figure 3a demonstrates that higher Rayleigh numbers tend to generate stronger convective currents, resulting in enhanced fluid movement and mixing. As the Rayleigh number increases, the Nusselt number reflects a more significant role of convective heat transfer, resulting in greater temperature differences across the fluid and more pronounced temperature gradients (refer to Figure 3b). Typically, higher Rayleigh numbers lead to increased heat transfer rates and more vigorous thermal mixing [31,34]. The convective currents and mixing associated with elevated Rayleigh numbers play a crucial role in altering entropy generation levels, which are particularly evident along the walls of the cavity, as shown in Figure 3.

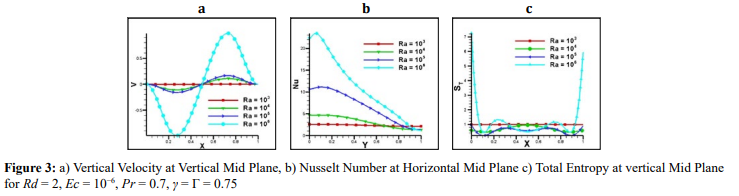
Effects of Radiation Parameter

Figure 4 shows streamline, isotherm, and total entropy isolines at fixed parameters Pr = 10, Ec = 10^-6, Ra=10⁶ , σ = 0.5, β =1 and γ =0.25 for various radiation parameters of (Rd=0,1,5,10). Streamlines are primarily determined by the fluid's motion and the forces acting upon it, such as pressure gradients and buoyancy. However, radiation influences the temperature allocation within the fluid, which consequently influences the density distribution and thus the flow patterns. Figure 4 shows that in the absence of radiation (Rd = 0) a double convective core regime is observed and this changes to a smooth and single circular core regime as radiation increases to Rd = 10. These effects are generally attributed to the fluid movements due to convective heat transmission. The effect on the isotherms as per our case is not showing much significance, this is due to the slow fluid movement caused by the viscoelastic nature of the Casson fluid parameter. Consequently, in figure 4 the isotherms are noticed to deviate as Rd increase which is solely based on the convection heat transfer. As radiation contributes to heat transfer, it as well impacts the local entropy production and distribution. Figure 4 shows that higher radiation levels can lead to increased heat transfer rates and entropy creation within the fluid. Entropy generation analysis is along the walls of the cavity for various radiation parameters.

Figure 5 depicts the variation of velocity, Nusselt number and overall, for distinct radiation parameters with Pr = 10, Ec = 10⁻⁶, Ra = 10⁶ , σ = 0.5, β = 1 and γ = 0.25. Radiation contributes to energy exchange within the fluid, resulting in changes in temperature distribution. These temperature variations will affect the fluid density, which in turn influences fluid motion and velocity. Changes in temperature due to radiation drives buoyancy forces and induce convective currents, altering the fluid velocity field as presented in figure 5a. The absorption of radiation by the fluid can increase its temperature, The Nusselt number is affected by the changes in temperature. Figure 5b shows that as radiation increases so does the Nusselt number. The absorption and emission of radiation can lead to local changes in temperature and therefore entropy production within the fluid, which is presented in figure 5c. Additionally, radiation can influence the entropy exchange between the fluid and its surroundings, contributing to changes in total entropy.

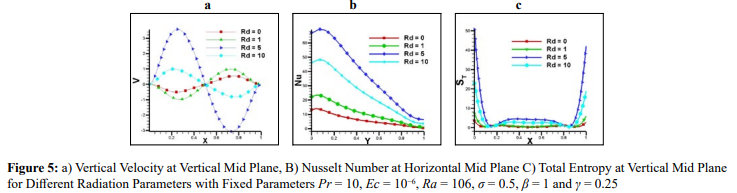
Effects of Prandtl Number

Figure 6 depicts streamline, isotherms and total entropy isolines for various Prandtl numbers at fixed parameters Ec = 10−6, Ra = 106 , Rd = 1,σ = 0.5, β = 1 and γ = 0.25. The Prandtl number affects the velocity distribution and the thickness boundary layer in a fluid flow. A higher Prandtl number implies a higher thermal diffusivity relative to the kinematic viscosity. As Prandtl changes from Pr = 0.1 to Pr = 10 the streamlines are more influenced by thermal effects than momentum effects. As a result, with a high Prandtl number, the boundary layer of velocity is thinner compared to the layer of thermal boundary. For isotherms, the temperature gradients in the fluid are less pronounced, and heat conduction is more dominant compared to convective heat transfer. Consequently, with a high Prandtl number, the isotherms tend to be smoother and less affected by convection (see figure 6). Similarly, for isolines of entropy, at a higher Prandtl number, the heat transfer is relatively more significant than momentum transfer. As a result, the isolines of entropy tend to be more aligned with the isotherms, reflecting the dominance of thermal effects in the system. Figure 6 shows that isolines cluster around the walls and become more pronounced as Prandtl changes from Pr= 0.1 to Pr= 10 [30,33]. Figure 7 presents velocity, Nusselt number and total entropy at fixed parameter are Ec = 10−6, Ra = 106 , Rd = 1, σ = 0.5, β = 1 and γ = 0.25. At high Prandtl number (Pr = 10), the velocity boundary layer becomes lean, and the velocity gradients near the solid boundaries are more pronounced (see figure 7a). The Prandtl number plays an important role in finding the Nusselt number. The Prandtl number appears as an exponent in the Nusselt number correlation, indicating its influence on convective heat transfer. Figure 7b shows that a higher Prandtl number generally leads to a higher Nusselt number, which enhanced the convective heat transfer. Entropy is createdIn a fluid flow because of both heat transfer and fluid friction (viscous dissipation). The ratio between heat transfer and fluid friction is affected by the influences Prandtl number. A higher Prandtl number implies higher thermal diffusivity relative to the kinematic viscosity. Consequently, with a high Prandtl number, the heat transfer effects dominate over fluid friction effects, resulting in a higher total entropy generation in the system (see figure 7c).

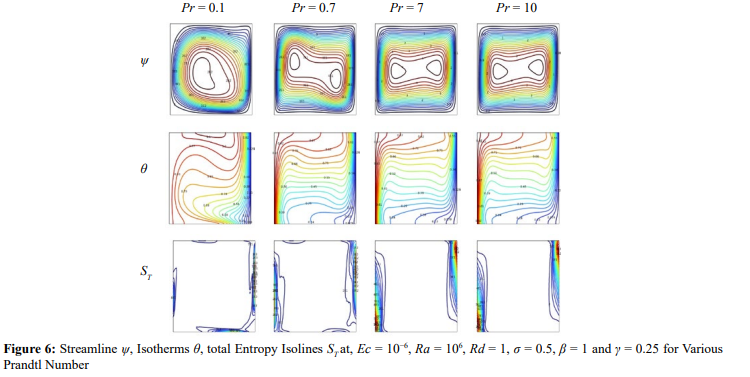
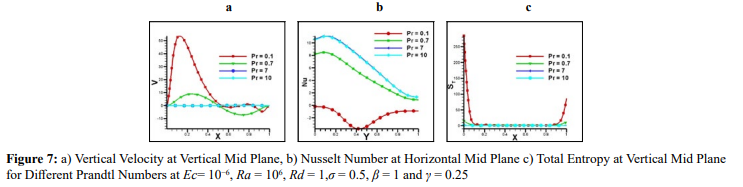
Effects of Casson Fluid Parameter

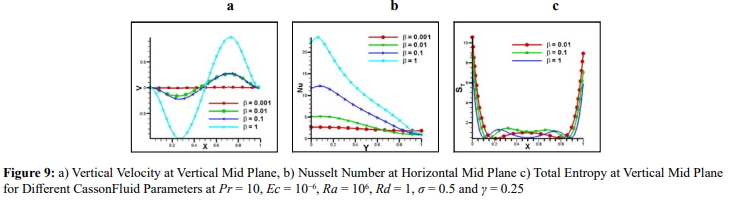
Streamline, isotherms, and total entropy isolines for various Casson fluid parameters at Pr = 10, Ec = 10⁻⁶, Ra = 10⁶ , Rd = 1, σ = 0.5 and γ = 0.25 are presented in figure 8.The Casson fluid parameters, particularly the yield stress, significantly influence the streamlines in the flow. The lowest stress needed to start a fluid flow is represented by the yield stress . In regions where the applied stress is below the yield stress, the fluid remains stationary, creating a stagnant zone. Figure 8 indicates that as Casson fluid parameter changes from β = 0.001 to β = 1 the convective cell cores change from smooth and circular single cell cores to chaotic and double cell cores. The Casson fluid parameters generally have a limited effect on the isotherms, as they primarily describe the rheological behavior of the fluid rather than its thermal characteristics. A near thermal stratification is observed for β = 0.001 and the isotherms changes significantly for β = 1 as the temperature gradients increase. This can result in local variations in the temperature distribution and potentially influence the alignment of the isotherms in those regions. The isolines of entropy in a Casson fluid flow tend to exhibit more pronounced gradients and deviations due to the additional energy dissipation and flow complexity associated with the yield stress behavior as the casson fluid parameter increase (see figure 8) [34]. Figure 9 depicts the velocity, Nusselt number and total entropy for various Casson fluid parameters with Pr = 10, Ec = 10⁻⁶, Ra = 10⁶ , Rd = 1, = 0.5 and γ = 0.25. Higher values of the Casson fluid parameter indicate a higher yield stress and a more significant resistance to flow. As a result, the velocity profile becomes more flattened near the boundaries, and the fluid tends to move with a higher velocity in the central region of the flow. The yield stress acts as a barrier, requiring a certain amount of shear stress to initiate the flow. Therefore, a higher Casson fluid parameter leads to reduced velocities near the boundaries and increased velocities in the core region of the flow (see figure 9a). Higher values of the Casson fluid parameter leads to lower Nusselt numbers, indicating a reduced convective heat transfer as observed in figure 9b. The presence of a yield stress and non-Newtonian behavior leads to additional energy dissipation and increased entropy generation. The Casson fluid parameter sways the behavior of flow, velocity gradients, and shear stresses in the fluid. Figure 9c shows that higher values of the Casson fluid parameter generally result in increased overall entropy creation in the flow due to the greater resistance and energy dissipation associated with the yield stress behavior.

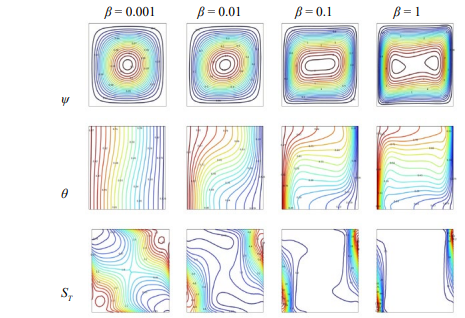
Figure 8: Streamline ψ, Isotherms θ, total Entropy Isolines ST at, Pr = 10, Ec = 10⁻⁶, Ra = 10⁶ , Rd = 1,σ = 0.5 and γ = 0.25 for Various β

Effects of Time

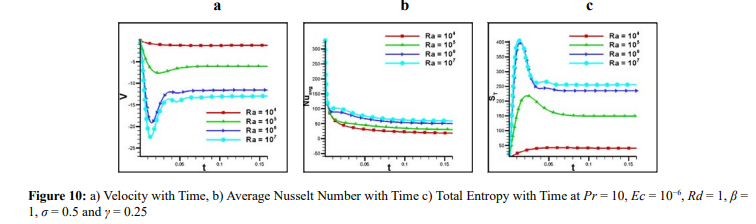
For varying Rayleigh values, the velocity,average Nusselt number, and over all entropy are presented against time in figure 10. The flow pattern increases over time with the Rayleigh number, the velocity diminishes and attained uniform flow phenomena. This is because, in convective heat transfer, velocity fluctuations promote the exchange of thermal energy between the fluid and solid surfaces, leading to enhanced heat transfer rates. In buoyancydriven flows, the Rayleigh number influences the changes in total entropy and average Nusselt number over time. When the flow starts, or the spread of temperatures varies the Nuavg and ST are observed to follow a uniform flow pattern as time evolves (see 10(b-c)).

Conclusion

Using the Finite Element Method, which provides accurate modeling and simulation capabilities, this study has effectively analyzed the characteristics of entropy generation in a porous medium containing Casson fluid during natural convection. The research has illuminated the complex interactions between fluid movement, heat transfer, and entropy creation within these systems. Through numerical simulations and analysis, it was demonstrated that parameters such as the Rayleigh number, Darcy number, Prandtl number, and Casson fluid parameter significantly influence the rate of entropy generation. The Casson fluid parameter, which accounts for the fluid's non-Newtonian behavior, notably affects flow and heat transfer properties. The Prandtl number evaluates the relative significance of heat transport compared to viscous effects, while the Darcy and Rayleigh numbers govern the intensity of natural convection. Additionally, the temperature distribution influences the average Nusselt number and total entropy, revealing a consistent flow pattern over time. As the Rayleigh number increases, the velocity of the flow pattern decreases, ultimately leading to a uniform flow state. The findings of this study enhance the fundamental understanding of fluid dynamics, entropy formation, and heat transfer. The incorporation of a porous medium will be emphasized, underscoring its significant impact on the behavior of the system.

Future research could build on this work by including additional coupled phenomena, such as chemical reactions, electromagnetic effects, or phase change processes, to better simulate complex real-world scenarios involving Casson fluids. This would enhance our understanding of applications such as electrochemical energy systems, and thermal management in phase-changing materials, thereby expanding the applicability and relevance of the findings. Similarly, extending the work by Integrating real-world experimental validation with numerical simulations will be for ensuring the reliability of FEM results, especially in practical fields such as food processing, pharmaceuticals, and energy systems. Experimental setups serve as precise benchmarks for numerical models by capturing intricate real-world phenomena, including non-Newtonian fluid behavior, thermal interactions, and boundary effects. This method not only bolsters the credibility of simulation predictions but also supports the development of optimized designs that address specific industry challenges and requirements.

References

1. Saboj, J. H., Nag, P., Saha, G., &Saha, S. C. (2023). Entropy production analysis in an octagonal cavity with an inner cold cylinder: a thermodynamic aspect. Energies, 16(14), 5487.
2. Saha, G., Al-Waaly, A. A., Paul, M. C., &Saha, S. C. (2023). Heat transfer in cavities: configurative systematic review. Energies, 16(5), 2338.
3. Pop, I., &Sheremet, M. (2017). Free convection in a square cavity filled with a Casson fluid under the effects of thermal radiation and viscous dissipation. International Journal of Numerical Methods for Heat & Fluid Flow, 27(10), 2318- 2332.
4. Hamid, M., Usman, M., Khan, Z. H., Haq, R. U., & Wang, W. (2019). Heat transfer and flow analysis of Casson fluid enclosed in a partially heated trapezoidal cavity. International Communications in Heat and Mass Transfer, 108, 104284.
5. Aneja, M., Chandra, A., & Sharma, S. (2020). Natural convection in a partially heated porous cavity to Casson fluid. International Communications in Heat and Mass Transfer, 114, 104555.
6. Aghighi, M. S., Ammar, A., &Masoumi, H. (2022). Doublediffusive natural convection of Casson fluids in an enclosure. International Journal of Mechanical Sciences, 236, 107754.
7. Shah, I. A., Bilal, S., Asjad, M. I., & Tag-ElDin, E. M. (2022). Convective heat and mass transport in Casson fluid flow in curved corrugated cavity with inclined magnetic field. Micromachines, 13(10), 1624.
8. Gireesha, B. J., Srinivasa, C. T., Shashikumar, N. S., Macha, M., Singh, J. K., &Mahanthesh, B. (2019). Entropy generation and heat transport analysis of Casson fluid flow with viscous and Joule heating in an inclined porous microchannel. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 233(5), 1173- 1184.
9. Kotha, G., &Chamkha, A. J. (2020). Entropy generation on convectively heated surface of casson fluid with viscous dissipation. PhysicaScripta, 95(11), 115203.
10. Sohail, M., Shah, Z., Tassaddiq, A., Kumam, P., & Roy, P. (2020). Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over nonlinear bi-directional stretching surface. Scientific Reports, 10(1), 12530.
11. Alzahrani, A. K., Sivasankaran, S., &Bhuvaneswari, M. (2020). Numerical simulation on convection and thermal radiation of Casson fluid in an enclosure with entropy generation. Entropy, 22(2), 229.
12. Hussain, S., Shoeibi, S., &Armaghani, T. (2021). Impact of magnetic field and entropy generation of Casson fluid on double diffusive natural convection in staggered cavity. International Communications in Heat and Mass Transfer, 127, 105520.
13. Seth, G. S., & Mandal, P. K. (2018). Hydromagnetic rotating flow of Casson fluid in Darcy-Forchheimer porous medium. In MATEC Web of Conferences (Vol. 192, p. 02059). EDP Sciences.
14. Qawasmeh, B. R., Alrbai, M., & Al-Dahidi, S. (2019). Forced convection heat transfer of Casson fluid in non-Darcy porous media. Advances in Mechanical Engineering, 11(1), 1687814018819906.
15. Farooq, U., Ijaz, M. A., Khan, M. I., Isa, S. S. P. M., & Lu, D. C. (2020). Modeling and non-similar analysis for DarcyForchheimer-Brinkman model of Casson fluid in a porous media. International Communications in Heat and Mass Transfer, 119, 104955.
16. Zhang, X., Yang, D., Israr Ur Rehman, M., & Hamid, A. (2021). Heat transport phenomena for the Darcy–Forchheimer flow of Casson fluid over stretching sheets with electro-osmosis forces and Newtonian heating. Mathematics, 9(19), 2525.
17. Li, S., Raghunath, K., Alfaleh, A., Ali, F., Zaib, A., Khan, M. I., ... & Puneeth, V. (2023). Effects of activation energy and chemical reaction on unsteady MHD dissipative Darcy– Forchheimer squeezed flow of Casson fluid over horizontal channel. Scientific reports, 13(1), 2666.
18. Raju, R. S., Reddy, B. M., & Reddy, G. J. (2017). Finite element solutions of free convective Casson fluid flow past a vertically inclined plate submitted in magnetic field in presence of heat and mass transfer. International Journal for Computational Methods in Engineering Science and Mechanics, 18(4-5), 250-265.
19. Reddy, G. J., Raju, R. S., & Rao, J. A. (2018). Influence of viscous dissipation on unsteady MHD natural convective flow of Casson fluid over an oscillating vertical plate via FEM. Ain Shams Engineering Journal, 9(4), 1907-1915.
20. Goud, B. S., Kumar, P. P., &Malga, B. S. (2020). Effect of heat source on an unsteady MHD free convection flow of Casson fluid past a vertical oscillating plate in porous medium using finite element analysis. Partial Differential Equations in Applied Mathematics, 2, 100015.
21. Rehman, K. U., Algehyne, E. A., Shahzad, F., Sherif, E. S. M., & Chu, Y. M. (2021). On thermally corrugated porous enclosure (TCPE) equipped with casson liquid suspension: Finite element thermal analysis. Case Studies in Thermal Engineering, 25, 100873.
22. Shahzad, H., Wang, X., Ghaffari, A., Iqbal, K., Hafeez, M. B., Krawczuk, M., &Wojnicz, W. (2022). Fluid structure interaction study of non-Newtonian Casson fluid in a bifurcated channel having stenosis with elastic walls. Scientific Reports, 12(1), 12219.
23. Khan, D., Khan, A., Khan, I., Ali, F., Karim, F. U., &Tlili, I. (2019). Effects of relative magnetic field, chemical reaction, heat generation and Newtonian heating on convection flow of Casson fluid over a moving vertical plate embedded in a porous medium. Scientific reports, 9(1), 400.
24. Alwawi, F. A., Alkasasbeh, H. T., Rashad, A. M., & Idris, R. (2020). MHD natural convection of Sodium Alginate Casson nanofluid over a solid sphere. Results in physics, 16, 102818.
25. Devi, T. S., Lakshmi, C. V., Venkatadri, K., Prasad, V. R., Bég, 25. Devi, T. S., Lakshmi, C. V., Venkatadri, K., Prasad, V. R., Bég,  O. A., & Reddy, M. S. (2020). Simulation of unsteady natural convection flow of a Cassonviscoplastic fluid in a square enclosure utilizing a MAC algorithm. Heat Transfer, 49(4), 1769-1787.
26. Anwar, T., Kumam, P., &Watthayu, W. (2021). Unsteady MHD natural convection flow of Casson fluid incorporating thermal radiative flux and heat injection/suction mechanism under variable wall conditions. Scientific Reports, 11(1), 4275.
27. Fusegi, T., Hyun, J. M., Kuwahara, K., & Farouk, B. (1991). A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure. International Journal of Heat and Mass Transfer, 34(6), 1543-1557.
28. Ho, C. J., Chen, M. W., & Li, Z. W. (2008). Numerical simulation of natural convection of nanofluid in a square enclosure: effects due to uncertainties of viscosity and thermal conductivity. International Journal of Heat and Mass Transfer, 51(17-18), 4506-4516.
29. Bayta¸s, A. C., and A. F. Bayta¸s.” Entropy generation in porous media.” Transport Phenomena in Porous Media III. Pergamon, 2005. 201-226.
30. Charreh, D., & Saleem, M. (2023). Entropy generation and natural convection analyses in a non-Darcy porous square cavity with thermal radiation and viscous dissipation. Results in Physics, 52, 106874.
31. Cham, B. M., Islam, S. U., & Islam, Z. U. (2024). Numerical study on natural convection in a saturated non Darcian porous medium under radiation and entropy generation effects. Applied Thermal Engineering, 123491.
32. Cham, B. M., Islam, S. U., & Islam, Z. U. (2024). Numerical study on natural convection in a saturated non Darcian porous medium under radiation and entropy generation effects. Applied Thermal Engineering, 123491.
33. Cham, B. M., Islam, S. U., Majeed, A. H., Ali, M. R., & Hendy, A. S. (2024). Numerical computations of magnetohydrodynamic (MHD) thermal fluid flow in a permeable cavity: A time dependent based study. Case Studies in Thermal Engineering, 61, 104905.
34. Cham, B. M., Shams-ul-Islam, S. U. I., Saleem, M., Talib, S., & Ahmad, S. (2024). Unsteady, two-dimensional magnetohydrodynamic (MHD) analysis of Casson fluid flow in a porous cavity with heated cylindrical obstacles. AIP Advances, 14(4).
35. Cham, B. M., & Sheikh, N. (2024). Fluid flow control around unequal cylinder spacing behind three side-by-side cylinders. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 46(10