Special Relativity and Absoluteness

Keywords: Special Relativity, Relative Absoluteness, Relativity Between Observers, Absoluteness of Coordinate Systems, Stationary System, Constant-Velocity System, Michelson–Morley Experiment, Light-Reciprocation Experiment, Doppler Effect, Twin Paradox.

1. Introduction

Physics describes physical motion in geometric terms, but physics and geometry differ in principle. While geometry is based on mathematical logic, physics must consider the physical conditions, even in thought experiments [1]. In particular, a physical coordinate system is determined by physical forces and requires physical definitions of rigid rulers, light rulers, and atomic clocks.

The four known fundamental forces are the strong nuclear force, weak nuclear force, electromagnetism, and gravity. In the presence or absence of gravity, a macroscopic coordinate system is called an inertial frame or gravitational system, respectively. A macroscopic inertial frame is found in regions of space distant from stars, where the gravitational forces sum to zero. In contrast, a macroscopic gravitational system exists in regions subjected to gravitational forces from stars.

After conducting a “thought experiment on a ship” Galileo Galilei introduced the principle of relativity to inertial frames in his Dialog Concerning the Two Chief World Systems, published in 1632 [2]. Newton’s Mathematical Principles of Natural Philosophy, published in 1687, posits that inertial frames are governed by inertial laws [3]. Since then, classical mechanics has accepted the Galilean transformation and its inverse, although the results of rigid rulers common to all observers are consistent with a relativistic Galilean transformation and its inverse. With respect to a static reference frame O, the moving system O₀' moves at constant speed v in the x-axis direction. Observers P''₁ (x'₁ ,y'₁ ,z'₁ ,t₁') and P''₂ (x'₂ ,y'₂ ,z'₂ ,t₂ ') in the moving system also pass at speed v with respect to observers P₁ (x₁ ,y₁ ,z₁ ,t₁ ) and P₂ (x₂ ,y₂ ,z₂ ,t₂ ) in the reference frame, where x_i , y_i , z_i, and t_i (i = 1, 2) denote the x-axis, y-axis, z-axis, and time, respectively. Because the coordinates of the inertial observer are linearly transformed, we can assume

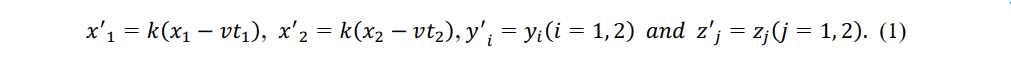
where k is only related to relative speed v and not to space or time coordinates. Because the length of a rigid rod is constant in an inertial frame, we have

In (1) and (2), the coordinates of observer P'' (x',y',z', t') in the moving system are seen by observer P (x,y,z,t) in the reference frame as

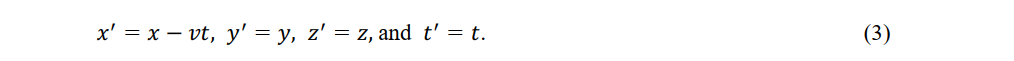
Equation (3) is the well-known Galilean transformation. Similarly, the coordinates of observer P (x,y,z,t) in the reference frame seen by observer P'' (x',y',z', t') in the moving frame are

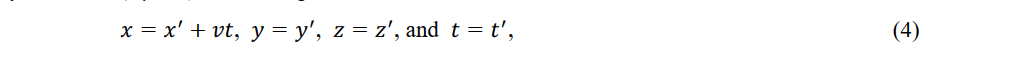
which is called the Galilean inverse. The Galilean transformation and its inverse depend on the length constancy of a rigid rod used by observers in both frames and represent absolute space and time.

Galilean transformations of classical mechanics were questioned during the development of electromagnetism. In 1886, Michelson–Morley conducted an interference experiment to discover ether, a space-permeable medium that is considered to be stationary in a vacuum. However, after applying the Galilean transformation, the experimenters failed to detect the expected wave interferences.4) In 1899, Lorentz proposed the Lorentz transformation based on the fact that the speed of light c remains unchanged after introducing a coordinate parallel to the direction of motion into Maxwell’s equations.5) In 1905, Einstein published his principle of special relativity, which states that physical laws are relative, whereas the speed of light is constant.6) Based on these two axioms, he also derived the Lorentz transform and its inverse.

With respect to the reference frame O, the moving system O′ moves at a constant speed v in the x-axis direction. Applying the laws of physics at constant c, the Lorentz transformation of an observer P' (ξ,η,ζ,τ) moving at constant velocity with respect to an observer P (x,y,z,t) in the reference frame is given by

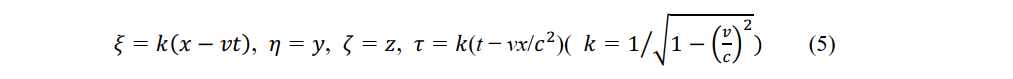
Applying the inverse Lorentz transformation to observer P' (ξ,η,ζ,τ) in the moving system, the coordinates of observer P (x,y,z,t) are obtained as

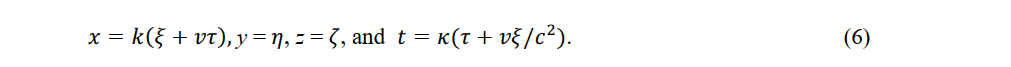
Equations (5) and (6) give the relative space and time coordinates between the reference-system observer P (x,y,z,t) and the moving-system observer P' (ξ',η',ζ',τ').

However, if we use a rigid ruler, the coordinates of the moving-system observers P' (ξ,η,ζ,τ) and P"(x',y',z',t') in (5) and (3), respectively, are related as follows:

Equation (7) shows that when measuring the length of an object in a constant-velocity system, a light ruler gives the same coordinates as a rigid ruler along the axis perpendicular to the movement direction, but k times longer coordinates than a rigid ruler along the axis parallel to the movement direction.

An inertial frame in which the lengths can be measured using a rigid ruler, light ruler, and an atomic clock is called a stationary system, whereas an inertial frame that allows only light ruler and atomic clock measurements is called a constant-velocity system. The relationship between coordinate systems is absolute. Observers in the common neighborhood of a stationary system and constant-velocity system use the same light rulers and atomic clocks, so their measurements are relative to each other. In an inertial frame, the absoluteness of the coordinate systems coexists with relativity between observers, which appears contradictory. Koh demonstrated that measurements using rigid and light rulers can distinguish a stationary system from a constant-velocity system.

Relativity between observers must be discriminated from the relativity of inertial frames. Relativity betwee observers denotes relativity between coordinates because two observers use the same light and atomic clocks, whereas relativity between inertial systems denotes relativity between inertial frames because both observers use a rigid ruler, light ruler, and atomic clocks. Einstein interpreted the relativity of physical laws as the relativity of the inertial frames. He overlooked the fact that rigid rulers can be used in reference systems (where the scales of a rigid ruler and a light ruler match) but not in moving systems (where the scales are mismatched) [8].

This study develops a space–time system of relativistic absolutism that integrates the absolute space–time concept of classical mechanics with the relative space–time concept of special relativity theory. Theoretically and methodologically, the author demonstrates how the absoluteness of the coordinate system coexists with relativity between observers in an inertial frame. First, a stationary system in the inertial frame is determined not through a wave-interference experiment, but through a light-reciprocation experiment in which the light-reciprocation time is constant only in stationary systems. Having determined the stationary system, the author describes the measurements of the stationary-point and moving-point coordinates. Next, the Lorentz transformation and its inverse are derived solely from the law of constant speed of light, which differs from the principle of special relativity [9]. The result showed that relativity of the laws of physics is not an independent axiom but a consequence of constant light speed.

Considering the rulers and clocks used by the observer, the author revealed that the absoluteness of the coordinate system and relativity between observers coexist in the Lorentz transformation and its inverse. The absoluteness of the coordinate system, which distinguishes a stationary system from a constant-velocity system, is proven by rigid ruler and atomic clock measurements. Meanwhile, the relativity between observers, which does not distinguish between stationary and constant-velocity observers, is proven by common light- and light-clock measurements. Although stationary system and constant-velocity system are mathematically relative, they are physically relative only in local areas.

Examples of observer–observer relativity are the transformation and inversion of the cosine of the direction of light when measured by different observers, principle of velocity addition, Michelson–Morley measurements, the transformation and inversion of electric and magnetic fields, Doppler effect, and energy conversion of light rays. These are described in the special theory of relativity, and the reason they are mentioned again is to correct them in terms of relativity between observers, not relativity between inertial systems. In an absolute coordinate system, a stationary system and a constant-velocity system can be distinguished by comparing the lengths measured by a rigid or light ruler, or by comparing the periods of atomic clocks in an inertial frame. The absoluteness of coordinate systems is exemplified by the results of the light-reciprocation experiment, absoluteness of an atomic clock, the twin paradox, normal direction of a reflecting mirror, and results of the electrostatic force experiments.

In Section 3, the difference between the accelerations of an object measured in a stationary system and a constant-velocity system is interpreted as the proximity effect of light. Charges are accelerated by electric or magnetic forces in a stationary system. The author explained how electric or magnetic forces in an instantaneous constant-velocity system can be converted to those in a stationary system. In other words, light from a light source that momentarily stops relative to a charge transmits force to the charge.

Although the acceleration and inertial forces acting on a charge are identical, the electromagnetic acceleration differs from the mechanical acceleration and the acceleration mass differs from the inertial mass. When a charge is accelerated under an electric force in a stationary system, it acquires acceleration mass m and a longitudinal inertial mass of K³ m. In addition, when an electric charge is rotated by a magnetic force in a stationary system, it acquires the same acceleration mass m, but a transverse inertial mass K² m.

In summary, assuming the constancy of a rigid rod, the law of the periods of atomic clocks, and the constancy of speed of light, a stationary system can be determined in an inertial frame, and a constant-velocity system can be constructed by deriving the Lorentz transformation. Examples of the absoluteness of the coordinate system and relativity between observers are presented, and the acceleration mass of an accelerated charge is shown to differ from the inertial mass in a stationary system with electromagnetic forces.

2. Methodology and Theory

Special relativity asserts that relative physical laws give rise to relative coordinate systems, whereas an absolute coordinate system coexists with relatively moving observers in an inertial system. To prove this assertion, one can analyze the Lorentz transformation and its inverse, assuming the physical invariance of a rigid ruler in the inertial system, the law of the periods of atomic clocks, and the constancy of light speed. Examples of the relativity of the observer and the absoluteness of the coordinate system are also presented.

2.1. Coexistence of Absoluteness and Relativity in an Inertial Frame

The Michelson–Morley interference experiment provided strong evidence for the relative space–time concept of special relativity. However, because light exhibits dual particle and wave behavior, wave interference and light-reciprocation experiment have different physical interpretations. To distinguish between a stationary system and a constant velocity system, light-reciprocation experiments, not wave interference experiments, is needed. Here, the author constructed a stationary system using a rigid ruler, a light clock, and an atomic clock, derived the Lorentz transformation and its inverse, and proved the absoluteness of the coordinate system and the relativity between observers.

2-1-1. Mechanical Stationary System

Kho (7) asserted that a stationary system can use a rigid ruler, a light clock, and atomic clocks, whereas a constant-velocity system is limited to light and atomic clocks. A light-reciprocation experiment in an inertial frame requires a light-reciprocation device composed of a light source, an observer, and a rigid rod with an atomic clock at one end and a reflecting mirror at the other end. If the length of the rigid rod is l and the speed of light is c, then the time of the light reciprocation is

If the light-reciprocation time remains constant at T₀ the system is stationary; otherwise, it is moving at constant velocity.[10]

Once the stationary system is determined, the coordinates of the stationary are measured. Assuming Euclidean geometry, the spatial coordinates of the stationary points are expressed in Cartesian coordinates, and their lengths are measured with a rigid ruler. The time coordinate of each stationary point is measured using a constant-wavelength atomic clock. Distant atomic clocks are synchronized with a rigid ruler and light. Synchronization introduced by Einstein is the phenomenon by which light emitted from a point P, where an atomic clock located at P reads t = t₀, reaches a stationary point Q at distance r from P and an atomic clock at Q is synchronized to

If we synchronize two atomic clocks using a rigid ruler and light, the point at which both clocks are stationary can be written as P (x,y,z,t). We also define a light ruler as a ruler that can measure the distance between the synchronized atomic clocks using a light beam.[11,12]. When the atomic clock located at source R reads t = t₁, the light from R reaches an observer S at time t = t₂. If the distance between the source R and the observer S is L, the light ruler measures.

Once the stationary point P(x,y,z,t) is determined, the coordinates of the moving point passing P must also be determined. As a moving point cannot be directly measured by an atomic clock or a rigid ruler, its coordinates are substituted with those of a nearby stationary point. A moving point P' is called P' (x,y,z,t) after passing the stationary point P(x,y,z,t) and P'(x+Δx,y+Δy,z+Δz,t+Δt) after passing the stationary point P1 (x+∆x,y+∆y,z+∆z,t+∆t). Einstein expressed the coordinates of a moving point as a function of time but did not mention replacing them with the coordinates of a nearby stationary point [13]. Substituting the coordinates of a moving point with the coordinates of a stationary point is equivalent to assuming an instantaneously stationary point near a permanently stationary point. By expressing the coordinates of the moving point as a function of time, we obtain the velocity and acceleration of the moving point. The measur velocity and acceleration in a stationary system are called the mechanical velocity and mechanical acceleration, respectively.

2-1-2. Electromagnetic Constant-Velocity System

Like a stationary system, a constant-velocity system contains stationary and moving points. The relationship between inertial frames is defined as a relationship between stationary points in the coordinate system. The relationship between a stationary observer P(x,y,z,t) and an observer P' (ξ,η,ζ,τ) passing nearby at constant velocity is derived using light beams in the stationary and constant-velocity systems. The rigid rulers, atomic clocks, and light clocks used by inertial observers are physically invariant.

By constancy of a rigid rod is meant that a rigid rod placed in a stationary system is invariant with respect to position and direction. If both ends of a moving rigid rod coincide with both ends of the rigid rod in a stationary system, the two rods are considered to have the same length. In addition, if the times at both ends of the rigid rod coincide, the lengths measured with the rigid and the light ruler always match.

Second, the periods of two atomic clocks are identical when both clocks are fixed in the same inertial frame but differ when the clocks are fixed in different inertial frames. Atomic clocks in stationary systems can be synchronized with a rigid ruler and light beams, but atomic clocks in constant-velocity systems must be synchronized with the atomic clocks in nearby-passing stationary systems.

Third, by constancy of light speed is meant that the speed of light measured during the light-reciprocation experiment in a stationary system always equals c. The lights from nearby light sources enter nearby observers and the speeds of light measured by the observer are c, regardless of the relative speed of the light source. The distance and time from the stationary observer to the origin of stationary light are defined as r and t, respectively, and the distance and time from a constant- velocity observer to the origin of a const nt-velocity light are r^' and t^', respectively. Then

Light propagates in the forward direction under the alternating actions of electric and magnetic fields. Therefore, although the light source and observer are stationary points, the light wave is a set of moving points. Accordingly, light propagates under proximate actions, and it appears to accelerate and decelerate with an average speed of c. When the light reaches the observer, it appears to arrive from a momentarily stationary light source.

As the rigid ruler, light, and atomic clock have well-defined physical invariants, only the constant light speed can ensure matching between a constant-velocity observer P' (ξ,η,ζ,τ) and a stationary observer P(x,y,z,t). A stationary light source O (0,0,0,0) and observer P(x,y,z,t) are fixed in the stationary system while a constant-velocity light source O^' (0,0,0,0) and observer P' (ξ,η,ζ,τ) are fixed in the constant-velocity system [14]. The light speed is c in both coordinate systems.

If x²+y²+z²=(ct)² is established, ξ²+η²+ζ²=(cτ)² is also established; conversely, if ξ²+η²+ζ²=(cτ)² is established, then x²+y²+z²=(ct)² is also established.

With respect to the stationary system O, the constant-velocity system O' moves at constant speed v in the x-axis direction:

Note that f(v) is not a function of x or t and that f(0) = 1. The source and observers are stationary in the constant-velocity system and the stationary system move with velocity ω along the ξ-axial direction i the constant-velocity system:

Note that g(-w) is not a function of ξ or τ and that g(0) = 1.

Based on the principle of the constancy of the speed of light, if x =ct, then it follows ξ=cτ and if x=ct, then it follows that ξ= cτ. By applying the two pairs of equations to (12) and (13) respectively, we obtain

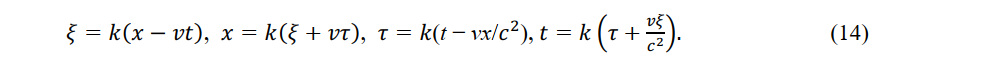
As the y-axis of the stationary observer at (x,y,z,t) and the η - axis of the constant-velocity observer P' (ξ,η,ζ,τ) are perpendicular to the direction of movement, another observer is seen to move at relative speed v.η = m (v)y and n(-v)η then hold. Moreover, m(0)=n(0)=1 so η = y. By the same argument, ξ = z.

Equation (14) and the above expressions are the Lorentz transformation of P' (ξ,η,ζ,τ). The relations

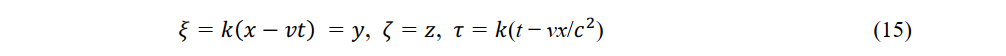
and

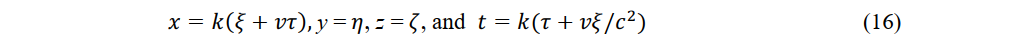
Are the inverse Lorentz transformations of P(x,y,z,t). Equations (15) and (16) were also derived by Lorentz and Einstein? The Lorentz transformation and its inverse are derived merely by assuming constant light speed c without assuming relativistic physical laws. The velocity and acceleration measured by an observer in a constant-velocity system using a light ruler and a light clock are called the electromagnetic speed and electromagnetic acceleration, respectively

2-1-3 Coexistence of the Absoluteness of Coordinate Systems and Relativity between Observers

The Lorentz transformation and its inverse derived from special relativity are those derived from relative absolute theory. However, the physical interpretations of the Lorentz transformation and its inverse differ between the two theories. The former is interpreted in terms of relativity and assumes constant light speed, while the latter assumes the constant length of a rigid rod, constant light speed, and the law of periods of atomic clocks.

The following concepts of space-time are interpreted differently from the perspectives of special relativity and relative absolute theory.

First, the principle of special relativity makes no distinction between a stationary system and a constant-velocity system, whereas relative absolutism posits that both types of systems can be distinguished using rigid rulers and light beams. In (7), it is assumed that the x^'-axis coordinate measured parallel to the movement direction with a rigid ruler is 1/k times smaller than the ξ-axis coordinate measured with a light ruler. To clarify this difference, consider two mathematically identical spheres: one in a stationary system and the other in a constant-velocity system. In the stationary system, the sphere is described by

Where R is the sphere radius. In the constant-velocity system at t = 0, the sphere ξ²+η²+ζ²=R² becomes the spheroid

with radii of R / (k, R, and R ).

Einstein interpreted that a rigid sphere with radius R in a constant-velocity system becomes a spheroid in a stationary system with its ξ axis reduced by a factor of l/k. However, Einstein recognized no difference between the lengths measured with a rigid ruler and a light ruler in a constant-velocity system. The sphere ξ²+η²+ζ²=R² is measured with a light ruler but a rotating ellipsoid is measured with a rigid ruler.

Second, unlike special relativity, relative absolutism distinguishes between an atomic clock and a light clock. In the inertial system, there is a fixed atomic clock in the inertial system and a light clock that moves at speed c. Stationary atomic clocks and constant velocity atomic clocks have different periods because they are fixed to the stationary and constant velocity systems, respectively. As seen in (7), if a plane ξ=0 (x=vt) is perpendicular to the x-axis, the time in this perpendicular plane is

That is, an atomic clock in a constant-velocity system runs 1⁄k times slower than an atomic clock in a stationary system. Light clocks, which use linear light traveling at speed c, are similarly divided into stationary and constant-velocity light clocks. The law of invariance of the speed of light applies to the stationary light clock and the constant velocity light clock, so they are relative. Although Einstein recognized that relative time is stablished through the use of light clocks b stationary and constant-velocity observers, he did not recognize that an atomic clock fixed in a constant-vlocity system is delayed by 1⁄(k) times from that of an atomic clock fixed in a stationary system [16].

Third, special relativity considers that the whole stationary system and the whole consent-velocity system are relative, whereas in relative absolute theory, relativity is limited to local regions of the stationary and constant-velocity system [17]. In deriving the Lorentz transformation and its inverse, the constant-velocity observer P' was assumed to be a stationary point in the constant-velocity system, but in reality, the constant velocity observer P' is a stationary point in the three-dimensional object moving at constant velocity. Here, the problem of defining the time of a three-dimensional object is raised. Since a stationary system is synchronized with a rigid ruler and light, all points in the stationary system are simultaneous. However, since the constant velocity system is synchronized with lights, all points in the three-dimensional object are not simultaneous. If two points P₁' (ξ₁,η₁ ζ₁,τ) and P₂' (ξ₂,η₂ ζ₂,τ) in the three-dimensional object are simultaneous, the time of two points P₁ (x₁,y₁ z₁,t₁) and P₂ (x₂ ,y₂ , z₂ ,t₂ ) passing through the two points P₁' and P₂' do not coincide. Since t₂-t₁=v/c² (x₂-x₁)=v/c² ∆x and light moves by proximity, if two points P₁ and P₂ of the stationary system are in the local region, then the three-dime sional object with the two points P₁' and P₂' is in the local region and can use the same time. The fact that the Lorentz transformation and its converse are established in the local region means that the relativity between observers applies in the local region.

The constant-velocity observers P' (ξ,η,ζ,τ) and P₀' (ξ+∆ξ,η+∆η,ζ+∆ζ,τ) become respectively the constant velocity observers P'' (ξ,η,ζ,τ+∆τ) and P₀'' (ξ+∆ξ,η +∆η,ζ+∆ζ,τ+Δτ). Given a stationary observer at P(x,y,z,t), a constant-velocity observer at P' (ξ,η,ζ,τ), another stationary observer at P₀ (x+∆x,y+∆y,z+∆z,t+∆t), and another constant-velocity observer at P₀'' (ξ+∆ξ,η+∆η,ζ+∆ζ,τ+∆τ), the instantaneous Lorentz transform and its inverse are set as follows in the local domain:

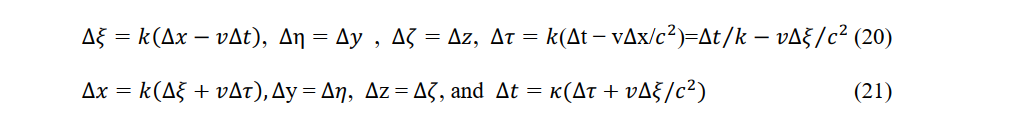
In an inertial frame, an absolute coordinate system is established macroscopically while relativity between observers is established locally.

2-2. Experiments on Relativity between Observers

Using light beams and atomic clocks for measurements in both stationary and constant-velocity systems, the Lorentz transformation and its inverse are derived and relativity between observers is established.

2-2-1. Transformation of Direction Cosines of Light and Their Inverse Transformation

One way to check relativity between observers is to compare the direction cosines of light measured by them.

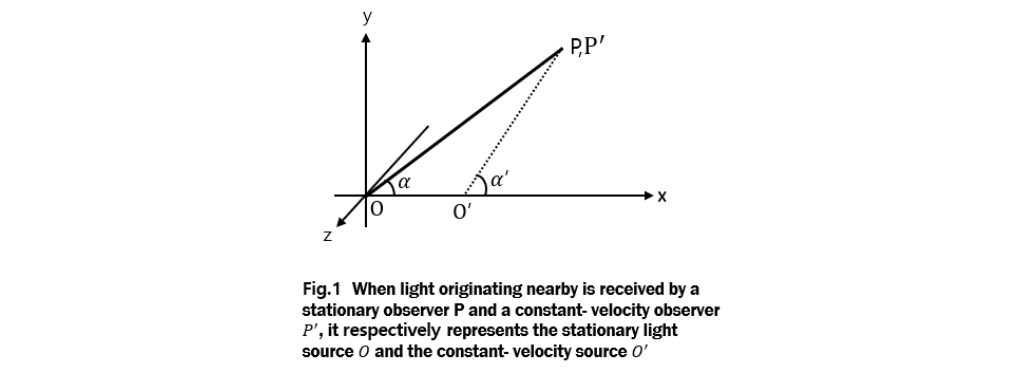
The light simultaneously emitted from a stationary source O and a constant-velocity source O_i^' travels linearly and reaches a stationary observer P (x,yx,z,t) and a constant-velocity observer P' (ξ,η,ζ,τ) in the vicinity. The cosines of the light directions measured by observers P and P' are cos α, cos β, cos γ, and cos α', cos β', cos γ' respectively.

Observer P observes the light from two light sources,O' and O. Applying the Lorentz transformation equation (15), the direction cosines of the two lights L' and L are related as follows [18].

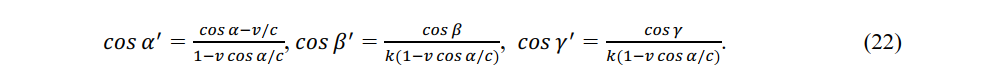
The time of light L^'  in the constant-velocity system is

Stationary observer P also observes the lights from O and O'. Using the Lorentzian inversion (16), the directional cosines of lights L and L' are related as

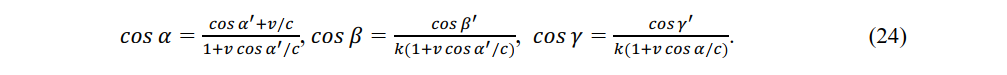
The time of light L in the constant-velocity system is

Equations (22) and (23) are conv rsion equations of the direction cosines of light and (24) and (25) are the inverse conversion equations.

When light of stationary system with direction cosines of cos α, cos β, cos γ, reaches constant-velocity observer P', the direction cosines are given as cos α', cos β', cos γ' by (22). Similarly, when light of constant-velocity system with direction cosines of cos α', cos β', cos γ' reaches a stationary observer, the direction cosines become cos α, cos β, cos γ, by (24). When an observer measures the speed of light from a relatively moving light source, the speed c remains constant but the direction and time of the light change. In a gravitational field, these changes are gradual but in an inertial frame, they appear to arrive from a light source that is momentarily stationary with respect to the observer [19].

2-2-2. Principle of velocity addition

In a stationary system, an object M' moves at a constant speed with

According to (15) and (16), a constant-velocity observer measures the speed of object M' as follows[20]

As (27) and (28) are derived from the Lorentz transformation and its inverse, the velocity addition principle is relative.

Let us consider an object M' moving at speed v in a stationary system. Setting V_x =v and V_y = V_z=0 in (27), we have

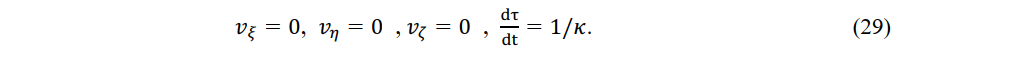
The time Δτ of an observer P₂' in a constant-velocity system moving with object M' is 1/κ times the time ∆t of an observer through which object M' passes.

Next, let us consider an object M fixed at the stationary system. Setting V_x = V_y = V_z=0, in (27), we obtain

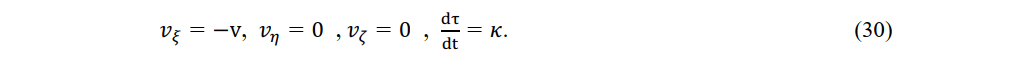
Although object M is fixed in a stationary system, for an observer P₁' with constent velocity v passing through object M, M is moving with − v with respect to itself as well as its time Δτ is k times M's time Δt.

In a stationary system, the moving object M' and the stationary object M have the same time, but the constant-velocity observer P₂' accompanying the object M' and P₁' passing the object M at speed v correspond to different times. In other words, object M' and M, which are simultaneous in a stationary system, are not simultaneous in a constant-velocity syst m. This means that the mechanical speed v measured by a stationary observer and the electromagnetic speed -v measured by a constant-velocity observer have different physical meanings. The mechanical speed of the stationary system and electromagnetic speed of the constant-velocity system, given by (27) and (28), respectively, satisfy the velocity addition principle. However, to determine the momentum and kinetic energy of an object, w require only the mechanical velocity measured in a stationary system.

2-2-3. Michelson–Morley Experiment

The Michelson–Morley experiment is regarded as strong evidence for relativity between inertial frames. However, the light-reciprocation experiment must be interpreted differently from a wave-interference experiment. In two experiments, the distance from the light source to the reflecting mirror is added to the distance from the reflecting mirror to the light source. In a light-reciprocation experiment, light is r garded as a particle and the distance is measured with a light ruler, and in a wave interference experiment, light is regarded as a wave and measured with a rigid ruler. The total distance traveled by the light beam in a light-reciprocation experiment depends on the cosine of the light’s direction, wherea he total distance traveled by waves in a wave-interference experiment depends on the length of a rigid rod.

When a parallel wave and a horizontal wave simultaneously return to the wave source at time τ, both waves have traveled twice the distance r from the wave source to the mirror, so their phase ime is τ−2r⁄c. As two waves simultaneously incident on the wave source have the same phase times, they superimpose, and no interference is detected [21]. In a stationary interference experiment, no phase difference occurs between waves traveling in two directions. Therefore, wave-interference experiments cannot distinguish between a stationary system and a constant-velocity system.

2-2-4. Transformation and Inversion of Electric and Magnetic Fields

The instantaneous Lorentz transformation and its inverse within a local region are exemplified by the transformations of electric and magnetic forces and their inverses. Let the measured electric and magnetic fields be (X,Y,Z) and (L,M,N), respectively, at a stationary origin O, and (X',Y',Z') and (L',M',N'), respectively, at the origin O' of a constant-velocity system. Applying the instantaneous Lorentz transformation (20) to Maxwell’s equations, th electromagetic field components in a constant-velocity system become

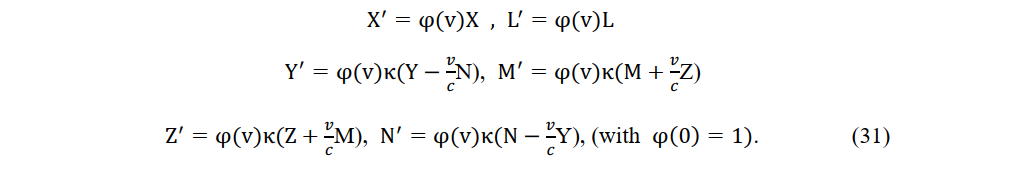
Applying the inverse Lorentz transformation (21) to Maxwell’s equations, the electromagnetic field components in a stationary system transform as

In (31) and (32), φ(ν)^. φ(-ν)=1. Considering the relativity of inertial fames, Einstein assumed that φ(ν) = φ(-ν), but this assumption is invalid in the absoluteness of the coordinate system

Since φ(0) = 1, φ(ν) > φ(-ν) is violated and φ(ν) < φ(-ν) cannot hold.[22].
Therefore,

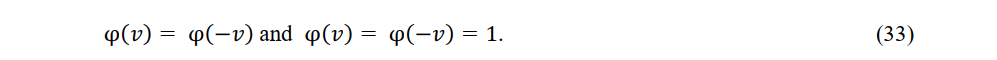
The electric and magnetic fields in (31) and (33) are transformed as follows:

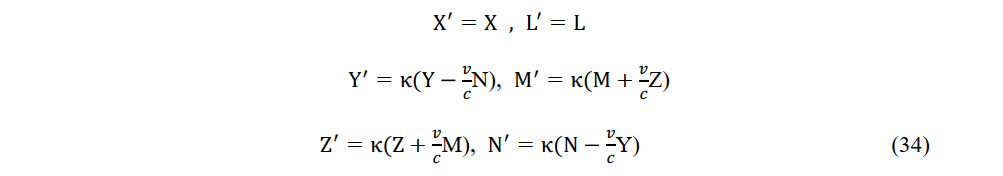
The inverse transformations of the electric and magnetic fields in (32) and (33) become

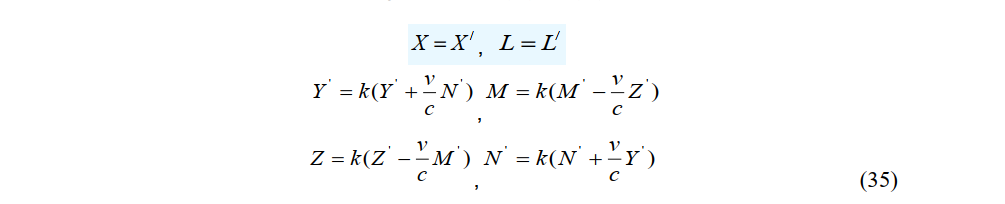
The transformed electric and magnetic forces and their inverses in the local domain of a stationary system are relative to those in the local domain of a constant-velocity system.

2-2-5. Doppler effect

Einstein assumed that an electrodynamic wave originates very far from the origin of a referenc system K. In a region of space contai ing the origin of coordinates, the electromag etic components can then be approximated as follows:

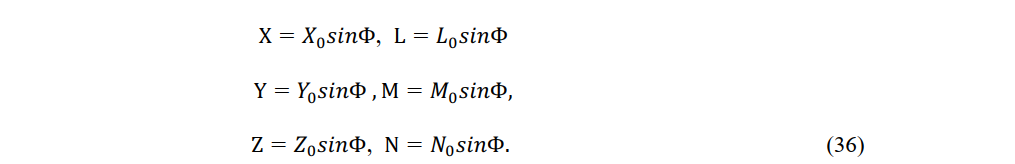
Here, (X₀,Y₀,Z₀) and (L₀,M₀,N₀) are vectors defining the amplitude of the wavetrain and cos α , cos β and cos γ are the directional cosines of the wave normal in reference system K.The phase of a wave emanating from a wave source fixed in reference system K is denoted by

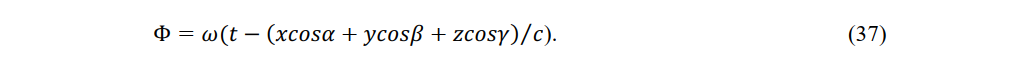
Applying the transformation equations of the electric and magnetic forces (31) and the transformation equations of coordinates and time (17), Einstein directly obtained [23].

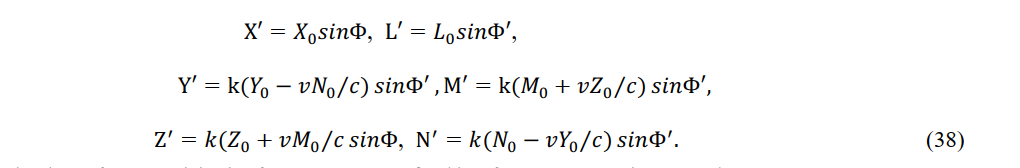
The phase of a wave originating from a wave source fixed in reference system K is measured as

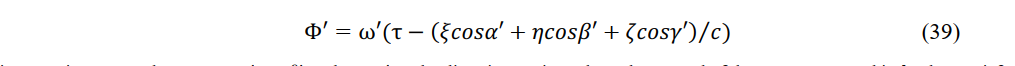
in a moving system k. Here, cos α' , cos β' and cos γ' are the direction cosines along the normal of the wave measured in k. They satisfy (22) and (23). The term ω' is given by

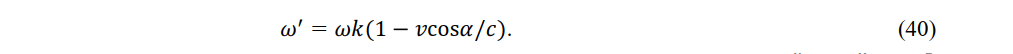
Light beams with direction cosines of cos α, cos β, cos γ travel along the straight line . There fore, an observer P(x,y,z,t) can observe the wave traveling in a straight line. The phase equation of a stationary system is given by

A constant-velocity observer P' (ξ,η,ζ,τ) can observe the wave 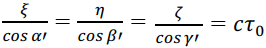traveling in a straight line. Similarly, the phase of a constant-velocity system can be written as

Accordingly, the frequency ν of the wave in the stationary system K is related to the frequency ν′ of the wave in the constant-velocity system K as follows:

2-2-6. Energy conversion of light rays

Einstein’s description of the energy conversion of light rays follows the Doppler principle. [24] Let the amplitudes of the electric and magnetic forces in a stationary system be A and A', respectively. The energy of light per unit volume in a stationary system is A²/8π. Considering the relativity between observers in an inertial frame, the amplitude of the electric and magnetic forces is A' and the energy of light per unit volume is A²/8π. The following equation then holds

If the cosines of the normal direction of the wave are cos α, cos β, cos γ, then no energy passes through the surface of a sphere traveling at the speed of light. Einstein posited the following equation for a sphere in a stationary system:

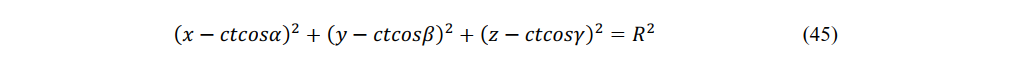
At time τ = 0 in a constant-velocity system, a sphere is described by

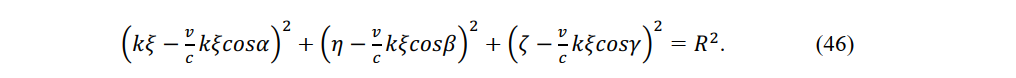
Considering that the energy of light is contained in a small sphere and that the light travels straight due to proximity action, the instantaneous Lorentz transformation should be applied to convert the energy of light. The equation of the sphere becomes

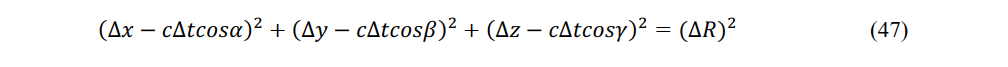
In constant-velocity system at ∆τ = 0, the sphere is described by

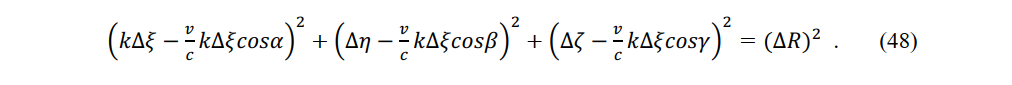
Let S and S' be the volumes of a sphere in a stationary system and a rotating ellipsoid in a constant-velocity system, respectively. Equivalently, let E and E' be the energies of the sphere and the rotating ellipsoid, respectively. Then we have

2-3. Experiments on the absoluteness of coordinate systems

In proving the absoluteness of the coordinate system, it was noted that the origin of the inertial system and the source of light in the inertial system are different. Moreover, in a stationary coordinate system, the origin and light source coincide, unlike those in the constant-velocity system.

2-3-1. Light-reciprocation experiment

When formulating his special relativity, Einstein derived the law of the constancy of the speed of light c from electromagnetism rather than from physical measurements. However, before building an inertial frame, c must be experimentally determined. The light-reciprocation experiment measures c in an inertial frame and thus determines the stationary system. When the light-reciprocation experiments are conducted in an inertial frame, the times of the light reciprocations are the same only in the stationary system. In a constant-velocity system, the time of the light reciprocation depends on the direction of the light movement relative to the direction of motion [25]. When measured with a stationary clock, the reciprocation times of light moving perpendicular and parallel to the motion are 2k r⁄c and 2k² r⁄c, respectively. When mea d with a constant-velocity clock, the former and latter times decrease to 2r⁄c and 2k r⁄c, respectively. During a reciprocation experiment of light in a constant-velocity system, the perpendicularly moving photons precede the photons moving parallel to the direction of movement.

2-3-2. Absoluteness of a Stationary Atomic Clock

As shown in (19), a constant-velocity atomic clock runs 1⁄k times more slowly than a stationary atomic clock. Stationary atomic clocks are the fastest among inertial atomic clocks. This is called the absoluteness of a stationary atomic clock. In other words, the period of a constant-velocity atomic clock is k times longer than the period of a stationary atomic clock. Therefore, we set t=kτ. (50)

This slowdown phenomenon is found in the decay cycle of elementary particles moving at near-light speeds. The decay period of a μ particle at the ground is t₀, but μ particles in air travel linearly at speed ν through a distance kvt₀, much longer than the expected distance vt₀, disappearing. The decay cycle of a μ particle moving at constant velocity is k times longer than that of a stationary μ particle.

2-3-3. Twin Paradox

The twin paradox is a thought experiment that probes the relativity of time through the Lorentz transformation and its inverse. The twin paradox erroneously overlooks the difference in synchronization methods between stationary and constant-velocity systems. The older of the two twins remains on Earth, while the younger brother rides a rocket traveling at speed v to a planet at dista ce vt₀ from Earth. The rocket then returns to Earth. The older brother notes that his younger brother appears 1/k times younger than his actual age, while the younger brother makes the same observation of his older brother.

The twin paradox violates the conditions under which the Lorentz transformation and its inverse can be derived in an inertial frame [26]. First, the premise that the older twin remains on Earth while the younger brother travels on a rocket at constant velocity does not conform to the inertial system because a rocket traveling at constant speed must pass the Earth without stopping. Second, as a rocket moving at speed v cannot change direction, it cannot return to Earth from a distant planet. Third, the atomic clocks of the Earth and the planet are synchronized with rigid rulers and light, so the times flow in a same manner.

To resolve the abovementioned problems, the twin paradox should be modified as the four-coeval paradox. At t=0, there are two coevals: the rocket coeval P' and the Earth coeval Q. At t=t₀, the number of coevals expands to four: a rocket coeval P' passing the planet coeval P and another rocket coeval Q' passing the Earth coeval Q. From the viewpoint of the planetary coeval P, the rocket coeval P' traveling at speed v passes at time τ = t/k and P' appears 1/k times younger. Meanwhile, from the viewpoint of the rocket coeval Q', the Earth coeval Q traveling at speed -v passes at time t=τ'/k and Q appears 1⁄k times younger.

Comparing the passing times of P' and Q above, the Earth and rocket systems appear to be relative with respect to time. However, because the Earth coeval Q and planetary coeval P are synchronized with rigid objects and light, the time flow of both coevals is t. Therefore, the rocket coeval P' passing the planet coeval P appears τ=t/k younger than the actual age, but the rocket coeval Q' passing the Earth coeval Q apparently ages by τ'=kt.The Twin paradox overlooks the simultaneous nature of the entire stationary system. Meanwhile, only a plane can be simultaneous in a constant-velocity system, so the Twin paradox is physically impossible.

2-3-4. Normal direction of reflective mirrors

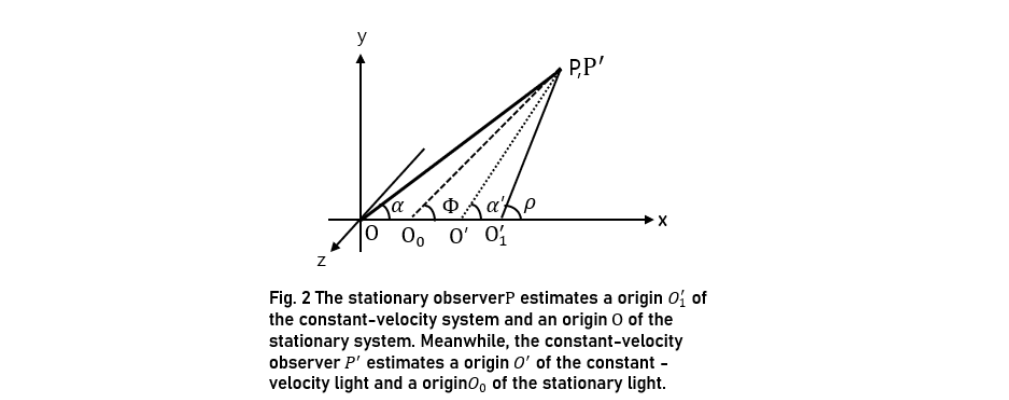
Recall that distances are measured using a rigid ruler in a stationary system and a light ruler in a constant-velocity system. Therefore, the origins of an inertial system measured by an observer P in a stationary system differ from those of an inertial system measured by an observer P' in a constant-velocity system. When light beams emitted from light sources in a nearby stationary and constant-velocity system reach a stationary observer P and a constant-velocity observer P' in the vicinity, four types of origins can be estimated. The stationary observer P estimates a origin O' of the constant-velocity system and an origin of the stationary system. Meanwhile, the constant-velocity observer P' estimates a origin O' of the constant -velocity light and a origin O₀ of the stationary light. The physical differences among the four origins can be confirmed through light-reciprocation experiments in an inertial frame.

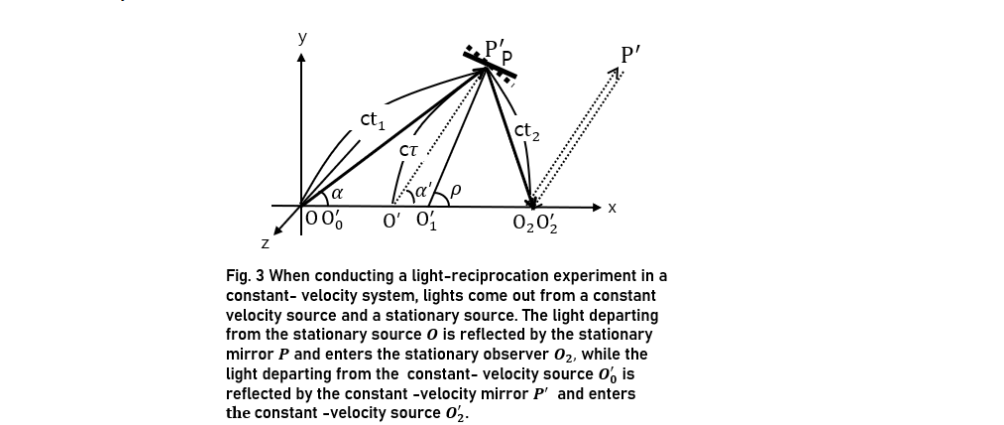
In light-reciprocation experiments in a stationary system, light from the source O of the stationary system and that from the constant-velocity source O₀' are reflected from the stationary mirror Q and constant-v locity mirror Q' and reach the source O in the stationary system and constant-velocity observer Q₃', respectively. The light leaving the source O with direction cosines of cos α,cos β,and cos γ reaches the mirror Q at time t. The reflected light then reaches the stationary source O with direction cosines of cos(π-α),cos β,and cos γ. Using (23), the light from the constant-velocity source O' moves by cτ₁=kct(1-(v⁄c)cos α) to the mirror O' and the reflected light moves by cτ₂=kct(1+(v⁄c) cos α ) to the constant-velocity observer O₃'. The time of this process is recorded as 2t by the observer O in the stationary system but as 2kt by the observer O₃' in the constant-velocity system. the same process is completed at time 2τ

The normal line of the constant-velocity stationary mirror P' is angled at α from the ξ-axis and the normal line of the stationary mirror P is angled at P from the x-axis. Therefore,

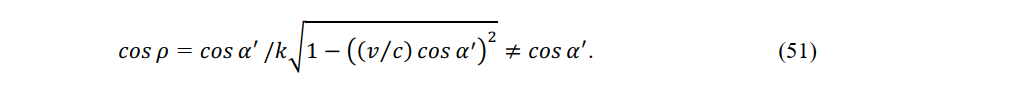
Meanwhile, the constant-velocity mirror and are separated by cτ but the mirror P and origin O₁' of the constant-velocity system are separated by a shorter distance

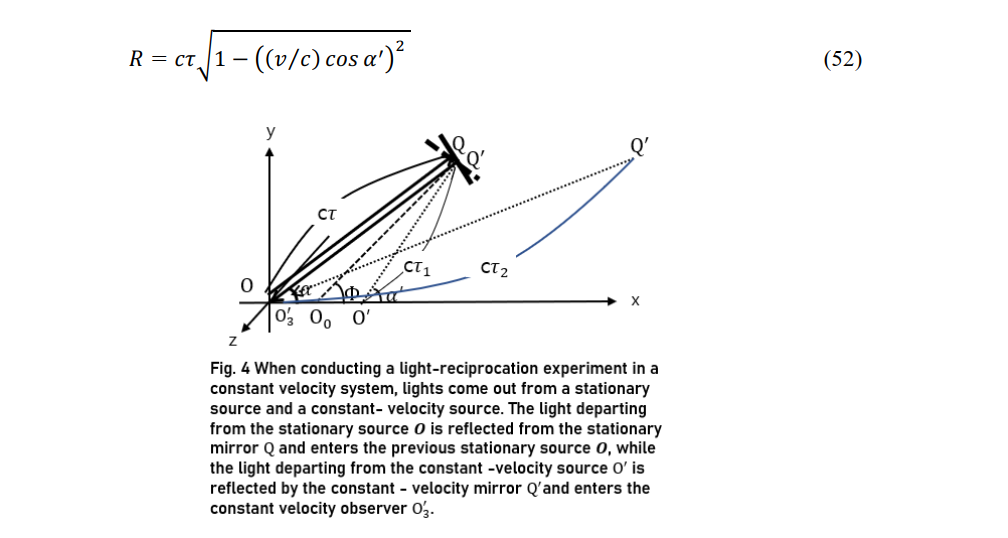
In light-reciprocation experiments in a stationary system, light from the source O of the stationary system and that from the constant-velocity source O₀' are reflected from the stationary mirror Q and constant-v locity mirror Q' and reach the source O in the stationary system and constant-velocity observer Q₃', respectively. The light leaving the source O with direction cosines of cos α,cos β,and cos γ reaches the mirror Q at time t. The reflected light then reaches the stationary source O with direction cosines of cos(π-α),cos β,and cos γ. Using (23), the light from the constant-velocity source O' moves by cτ₁=kct(1-(v⁄c)cos α) to the mirror O' and the reflected light moves by cτ₂=kct(1+(v⁄c) cos α ) to the constant-velocity observer O₃'. The time of this process is recorded as 2t by the observer O in the stationary system but as 2kt by the observer O₃' in the constant-velocity system. the same process is completed at time 2τ

The normal line of the stationary mirror Q is angled at α from the x-axis and the normal line of the constant-velocity mirror Q' is angled at Φ from the ξ-axis. Therefore,

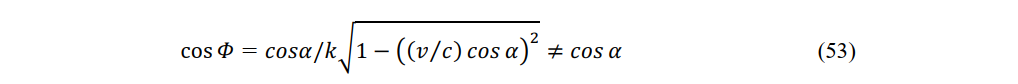
The stationary mirror Q and light source O are separated by O' and origin O₀ are separated by a shorter distance under the principle of constant velocity of light.

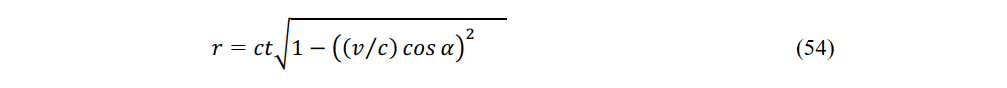
At orgin O₂' the constant-velocity system, where the time was recorded as 2τ, the light in the stationary and constant-velocity systems moved through distances of 2kcτ and 2cτ, respectively. At observer in the stationary system, where the time was recorded as 2t, the light in the stationary and constant-velocity systems apparently moved through distances of 2ct and 2kct, respectively. Comparing these two cases, the stationary and constant-velocity systems appear relative but the distance between the sources of the stationary and constant-velocity systems is 2kvτ in the former case and 2vt in the latter. Therefore, the stationary and constant-velocity ystems are unambiguously distinguished.

2-3-5. Electrostatic force experiments

When two charges are stationary with respect to each other, the stationary and constant- velocity systems can be determined by measuring the electrostatic force between the harges. The distance and electromagnetic force between the charges are measured with a rigid ruler and a light ruler, respectively.

An experiment is conducted to measure the electrostatic force acting between two charges fixed in a stationary system. As the electric charge Q₁ is at th origin O(0,0,0,0) of the stationary system and the electric charge Q₂ is fixed at the stationary system observer P(x,y,0,0), Coulomb’s law is applied. The force mutually acing between the two charges is given by

If the distance between two charges is the same, the electrostatic force is the same regardless of the direction in which the two charges are placed. As the results of both rulers coincide in a stationary system, the electrostatic force in a stationary system is independent of the direction of the two charges [27].

Next, an experiment is conducted to measure the electrostatic force acting between two charges fixed to the isokinetic meter. Consider a charge Q₁ placed at the origin O'(0,0,0,0) of a constant-velocity system and a charge Q₂ placed at an observer P(ξ,η,ζ, τ) (in the constant-velocity system. Suppose that Q₂ passes the origin O'(0,0,0,0) of a stationary system while Q₂ passes observer P(x,y,0,0) in the stationary system. Observer P' measures the electromagnetic force vector E(X',Y',Z') generated by Q_i. Measured by the light ruler, the coordinates of the charges are given by

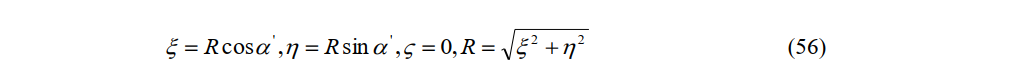
and the distance between the charges is

According to an observer in the constant-velocity system, the stationary observer travels at speed-v along the x-axis. Applying the inverse transformations of the electric and magnetic forces (34) to (57), we obtain

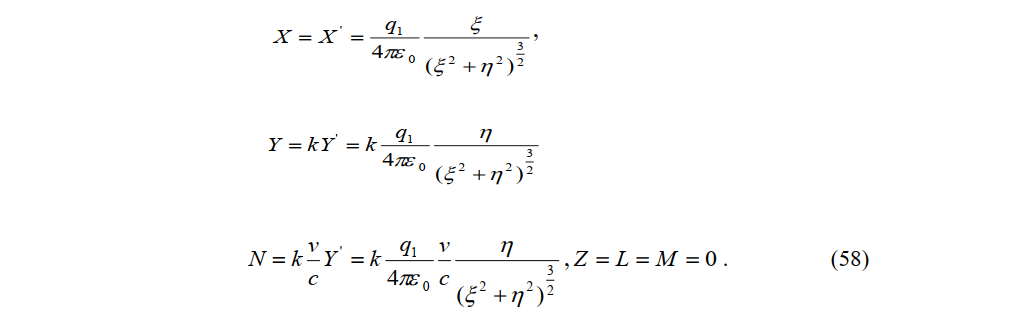
Meanwhile, ξ=kx, η=y, ξ=0, τ=-vkx/c² are obtained from the Lorentz transformation using Equation (15) , when t = 0.

Substituting this result into (58) yields the electric and magn tic forces measured by the stationary observerP

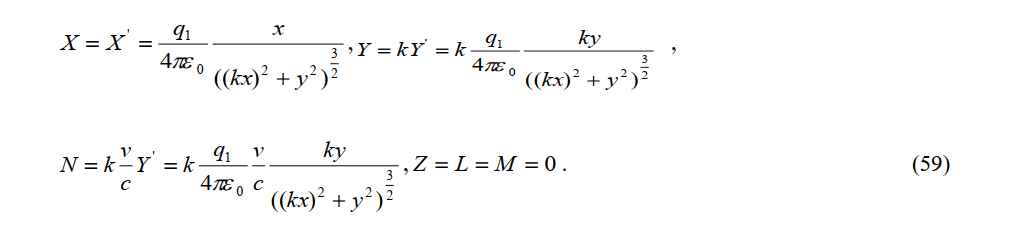
The charge Q measured by observer P'' in the constant-velocity system is associated with a Biot-Savart force induced by (59) at the stationary observer P'. The electric and magnetic force vectors measured by the stationary observer P are E and A, respectively. The force on charge Q₂ is then given by

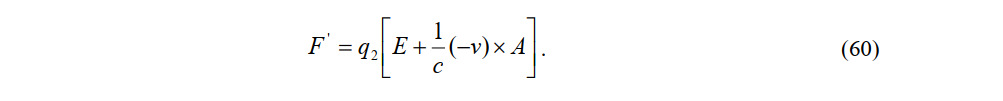
The force between charges and in the constant-velocity system depends on the velocity v of the constant-velocity system and the angle α between the straight line connecting the two charges and the x-axis:

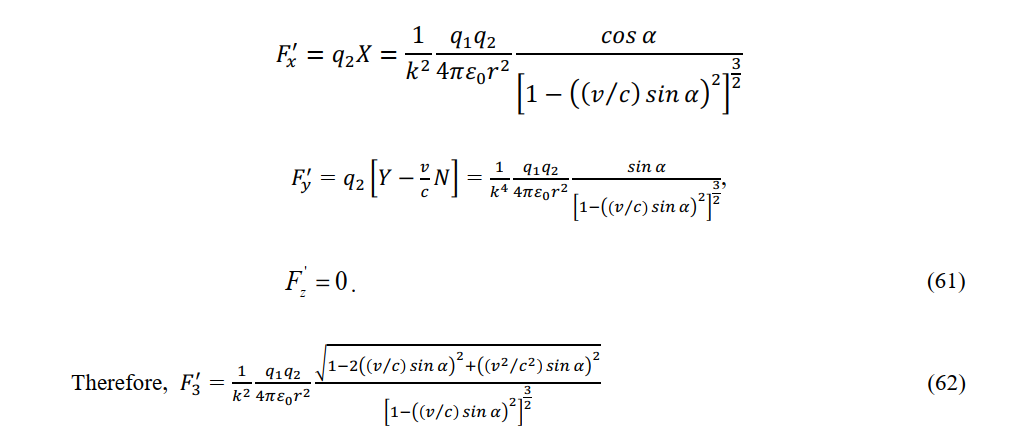
The minimum and maximum values of 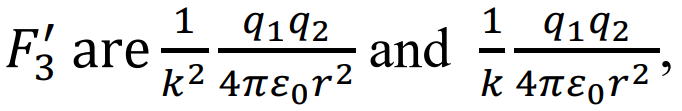respectively. occurring at α=0 and α=Π/2. respectively.

In a stationary system, the electromagnetic force between two charges is isotropic and given by Coulomb’s equation . In a constant-velocity system, the electromagnetic force becomes

 

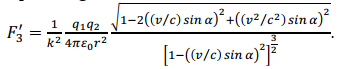
A stationary and constant-velocity system can be experimentally distinguished by studying electrostatic forces in an inertial frame.

The absolute space–time system of Newton’s classical mechanics can be integrated with the relative space–time concept of Einstein’s special relativity. The coexistence of an absolute coordinate system and relativity between observers has been demonstrated based on three axioms: the constancy of rigid rulers, the law of the periods of atomic clocks, and the constancy of light speed. In other words, a stationary system and constant-velocity system are distinct in a macroscopic inertial frame, but a stationary observer and a constant-velocity observer are relative within a local region.

3. Results and Discussion

The previous sections revealed that relativity between observers coexists with the absoluteness of a coordinate system in an inertial frame. The relativity between observers is enabled by the common use of light and atomic clocks in stationary and constant-velocity systems, whereas the absoluteness of the coordinate system results from the allowed use of rigid rulers in a stationary system, which cannot be used in a constant-velocity system. This section explores the mismatch between the accelerated and inertial masses when an object is accelerated in an inertial frame and the effects of accelerated motion under electric and magnetic forces on time and space.

3-1. Mismatch between inertial and accelerated mass in a local inertial frame

When an object is accelerated by an electromagnetic force in an inertial frame, the Galilean transformation is inapplicable because the mass changes.
The instantaneous Lorentz transformations (20) relate the velocity of a moving charge in a stationary system o the velocity of that charge in a constant-velocity system:

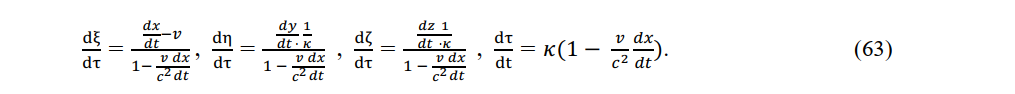
The acceleration of a charge in an electromagnetic field in a stationary system is related to the acceleration of that charge in a local area as follows:

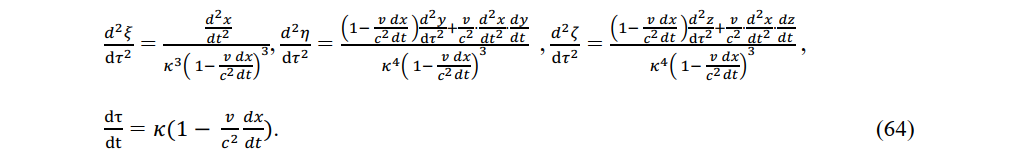
While the charge is accelerating, nearby light is transmitted to the observer at constant instantaneous velocity c, as though the light is being transmitted from a stationary source. That is, dx/dt=v and

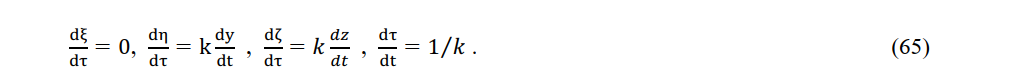
The acceleration of a charge in an electromagnetic field in a stationary system is related to the acceleration of that charge in a local area as follows:

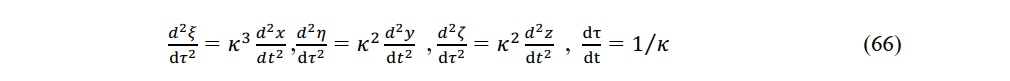
From (65) and (66), we note that although . This means that the charge is accelerated by the electric field of the stationary system, but it appears to be accelerated by the electric field of the constant-velocity system, which is actually stationary with respect to the charge.

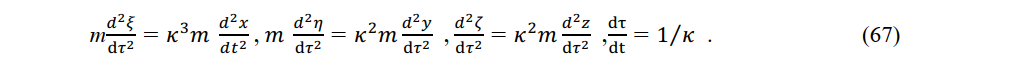
If an object of stationary mass m is accelerated and then moves at constant velocity v , how does one define its momentum? The definition of momentum differs between the Galilean and Lorentzian transformations. In the Galilean transformation, an object of stationary mass m retains that mass during acceleration to a constant speed. If the stationary time is t, the constant- velocity time is also t, so the momentum is

When an object accelerates in an inertial frame, its mass changes and the Galilean transformation is inapplicable.

In the Lorentz transformation, if the stationary system time is t, the constant velocity system time is different as τ = t> / k. As a stationary charge is accelerated by an electric field, its mass M will increase. The definition of momentum in a stationary system is P = Mv.

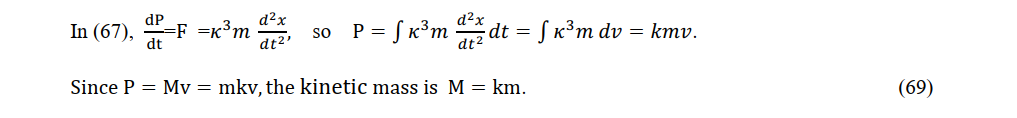
The kinetic mass, which is k times the stationary mass, is related to the time of the moving atomic clock, which is 1/k times slower than the stationary atomic clock.

I now show that when an electric force acts parallel to the direction of motion of a charge, an inertial force acts in the opposite direction. In (66), the electrodynamic acceleration d² ξ/dτ² due to an electric force is ³ times greater than the mechanical acceleration (d²x/dt² due to inertia. In (67), the acceleration mass on which the electric force acts is m and the longitudinal inertial mass on which the inertial force acts is k3m. Einstein referred to the longitudinal inertial mass k³m as the longitudinal mass [29]. To ensure constancy of the speed of light, electromagnetic acceleration acts in the instantaneous constant-velocity system and mechanical acceleration acts in the opposite direction in the stationary system. However, because the space–time of a stationary system is different from that of a constant-velocity system, the longitudinal inertial mass on which the mechanical acceleration acts is k3 times the rest mass on which the electromagnetic acceleration acts.

Moreover, if the magnetic force acts as a centripetal force perpendicular to the moving direction of the charge, it will be exactly opposed by the inertial force.

The magnetic acceleration d² η/dτ² in (66) induced by the magnetic force is κ² times greater than the mechanical acceleration (d² y)/dτ² due to the inertial force. The acceleration mass on which the magnetic force acts is m and the transverse inertial mass on which the inertial force acts is κ²m. Einstein referred to the transverse inertial mass κ²m as the transverse mass [30]. To ensure the constancy of the speed of light, the mechanical acceleration acting on the transverse inertial mass κ²m must oppose the magnetic acceleration of the charge.

3-2. Charge Accelerated By an Electric Field in a Stationary System

From (34) and (67), we obtain [31].

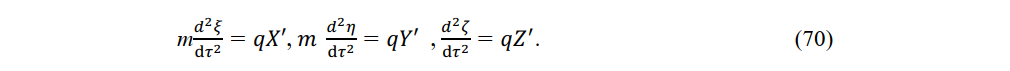
When a charge q is accelerated by an electric field in a stationary system, it experiences that electric field in a constant-velocity system moving at instantaneous speed v. When light from a stationary source reaches a charge moving at v, the electric force appears to arrive from a constant-velocity source. From (34), (67), and (70), the force on a charge accelerated parallel to the direction of motion is given by

Setting

we obtain

The velocity of a charge accelerated by a stationary electromagnetic field is

Equation (74) shows that the velocity of an object accelerated under electric forces in an inertial frame cannot exceed the speed of light.

 

3-3. Charges rotating due to a magnetic force in a stationary system

The magnetic force in a stationary system acts perpendicularly on a charge k moving at speed v. Rotation is induced by the Lorentz force. From (34) and (67), we have ..............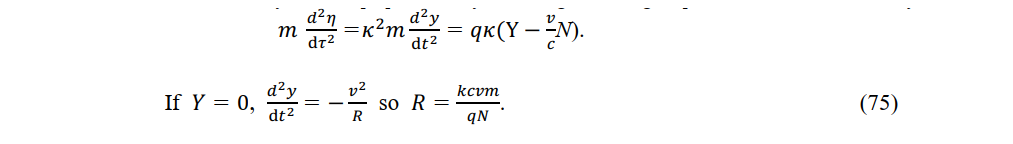

When a magnetic force in a stationary system acts perpendicul rly on a charge moving at speed v, it behaves like a magnetic force in a constant-velocity system and the gyration radius increases.

When a charge is accelerated due to an electromagnetic force in an inertial frame, the acceleration and inertia forces are equal.

The acceleration mass measured in an instantan ous velocit system is m but the inertial mass measured in a stationary system depends on the direction of the electromagnetic force. More specifically, the longitudinal and transverse inertial masses measured in a stationary system are k³ m and κ² m, respectively.

4. Conclusions

This paper integrates the absolute space–time concept premised on classical mechanics, the Galilean transformation and its inverse, and the relative space–time concept based on special relativity theory, the Lorentz transformation and its inverse. Akin to the wave–particle duality, relativity between observers coexists with the absoluteness of a coordinate system in an inertial frame. The theory underlying such a space–time system is called relative absoluteness to distinguish it from the theory of special relativity.

Relativity between observers can coexist with the absoluteness of the coordinate system because measurements in a stationary system are made with rigid rulers, light, and atomic clocks, although only light rulers and atomic clocks can perform measurements in a constant-velocity system.

Accordingly, this paper defines physical invariants related to rigid rulers, atomic clocks, and light rulers. The first principle is the constancy of a rigid rod, meaning that the length of a rigid rod (whether stationary or moving) is constant in an inertial frame. If the ends of two relatively moving rods coincide, the lengths of the two rods are equal. The second principle states that the periods of atomic clocks are invariant when fixed in an inertial frame but differ for atomic clocks in relative motion. Stationary atomic clocks are synchronized with rigid rulers and light, but constant-velocity atomic clocks are synchronized with light. Finally, the law of constant light speed means that the speed of light measured in the light-reciprocation experiment in a stationary system is constant at c, and the speed of light is always c, regardless of whether the light source is at rest or in motion relative to the observer.

The absoluteness of a coordinate system is proven using rigid rulers or atomic clocks. In an inertial system, the measurements of a rigid ruler and a light ruler will coincide in a stationary system and deviate in a constant-velocity system. Moreover, an inertial system with the fastest atomic clock becomes a stationary system; other inertial systems become constant-velocity systems. The absoluteness of coordinate systems is demonstrated by the light-reciprocation experiment, atomic clocks, the twin paradox, the normal direction of reflective mirrors, and the results of electrostatic force experiments.

Relativity between observers in nearby inertial systems is established by the commonality of light clocks. A stationary system is entirely simultaneous, but a constant-velocity system is simultaneous only in a plane. Therefore, relativity between observers is established only in local areas of the inertial system. Relativity between observers can be observed in the transformation of direction cosines of light and their inverses, velocity addition, the results of the Michelson–Morley experiment, the transformation and inversion of electric and magnetic fields, the Doppler Effect, and energy conversion of light rays.

In an inertial frame, the light source and observer are stationary points, but light is propagating at an average speed c with momentary accelerations and decelerations. The light incident on an observer appears to arrive from a momentarily

stationary light source. When a charge is accelerated in a stationary electromagnetic field, the acceleration measured in an instantaneous constant-velocity system differs from that measured in a stationary system. Of course, the acceleration force measured in an instantaneous velocity system equals the inertial force measured in a stationary system, so the acceleration mass in the instantaneous velocity system differs from the inertial mass in the stationary system; moreover, the longitudinal and transverse inertial masses differ.

This study focused on revealing the coexistence of relativity between observers and the absoluteness of coordinate systems based on the three axioms. Therefore, it was not possible to reveal the relation between the law of invariance of rigid rod, the law of the periods of atomic clocks and invariance of the speed of light. The following questions arise in relation to the three axioms. What is the relation between the increase in the period of an atomic clock and the electrostatic force acting between two stationary charges in a constant-velocity system? What is the relation between the increase in the period of an atomic clock and the invariance of the length of a rigid rod? What is the relation between measuring time and space using solid rulers, light, and atomic clocks and the uncertainty principle? Additionally, the author believes that just as general relativity was established based on the theory of special relativity, general relativity and absoluteness should be established based on special relativity and absoluteness.

References

1. Einstein, A., Lawson, R. W. (2016). Relativity Trans by Red and Black Publishers, Florida p. 6.
2. Newton, I. (1999). The Principia: mathematical principles of natural philosophy. Univ of California Press.
3. Galilei, G. (1967). Dialogue concerning the two chief world systems. first published in, 1632, 891-921.
4. Michelson, A. A., Morley, E. W. (1887). Am. J. Sci. s3–34, 333.
5. Lorentz, H. A. (1904). Proc. R. Netherlands Acad. Arts Sci. 6, 809.
6. Miller, A. I. (1981). Albert Einstein's Special Theory of Relativity: emergence (1905) and early interpretation (1905-1911) (pp. 47-54). Reading, MA: Addison-Wesley.
7. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electron Eng, 2(1), 31-40.
8. Miller, A. I. (1981). Albert Einstein's Special Theory of Relativity: emergence (1905) and early interpretation (1905-1911) (pp. 47-54). Reading, MA: Addison-Wesley.
9. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 35.
10. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 33.
11. Miller, A. I. (1981). Albert Einstein's Special Theory of Relativity: emergence (1905) and early interpretation (1905-1911) (pp. 47-54). Reading, MA: Addison-Wesley.
12. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 33.
13. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 393.
14. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 35.
15. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 401.
16. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 394.
17. Einstein, A. (2016). Relativity Trans by R. W. Lawson (Red and Black Publishers, Florida) p. 31.
18. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 407.
19. Einstein, A. (2016). Relativity Trans by R. W. Lawson (Red and Black Publishers, Florida) p. 142.
20. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 402.
21. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 39.
22. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 405.
23. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 407.
24. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 409.
25. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 38.
26. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 38.
27. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 28.
28. Koh, H. (2023). Coexistence of Relativity between Observers and the Absoluteness of Inertial Systems. J Electrical Electronics Eng, 2(1), p. 30.
29. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 414.
30. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 414.
31. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 413.
32. Miller, A. I. (1981). Albert Einstein’s Special Theory of Relativity, on the Electrodynamics of Moving Bodies Einstein. Addison-Wesley Publishing Company, Massachusetts, p. 415.

Copyright: ©2023 Hyoungseok Koh. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.