The Unified theory of Numerical Polarity

Introduction

The author of this article started his career as a self-taught, self- employed C&I engineer, metamorphosing himself in about 2007 into a self-taught, self-employed quantum physicist. This self- teaching of quantum physics has led him into changing his career once again into becoming a teacher of the superior arithmetical logic required in quantum physics. We need this superior arithmetical logic in order to obtain a grip upon Quantum-Relativity. Except with the subject of Quantum Relativity, our arithmetical concepts can remain rather sloppy, for Quantum-Relativity we must rid our arithmetical thinking of all logical sloppiness. This tightening up of our arithmetical logic, feeds back positively into our understanding of everything else, specially in nuclear physics, astrophysics, cosmology and even with the science of money.

 Who amongst us are Numerate?
Numeracy is the human appreciation of the relative scale of things using numbers. We are so familiar with the decimal system of counting that we can hardly express any numbers at all without reverting to the serial expression of decimal characters in ten-base exponential strings, but that is of course not good enough for a computer theorist. The decimal number 123 means 1 x 10^2 plus 2 x 10^1 plus 3 x 10^0. The decimal number 123 can be equally well expressed in binary as 111 1011, which means 1 x 2^6 + 1 x 2^5 + 1 x 2^4 + 1 x 2^3 + 0 x 2^2 + 1 x 2^1 + 1 x 2^0. Notice that both identical expressions of the same number are the sum of either a 10-base exponential string or a 2-base exponential string. We could think about the absurd one-base string and the expression there would just be one hundred and twenty three ones in a row, which would take up a lot of space, so I will not write that out here, but if I did that, it would be valid. It is only in the absurd 1-base case that we can never express a fraction. For example; 12.3 means 1 x 10^1 + 2 x 10^0 + 3 x 10^-1 which in binary is 1100.0100 1100 1100 1100 1100….. In binary counting, the decimal fraction 0.3 is irrational, the binary exponential string of (decimal) 0.3 can never terminate.

Before modern number theorists took charge of the teaching of mathematics in about 1973, what I have just explained above was common knowledge, taught to me aged 13 in a STEM focused grammar school in 1963. The decimal fraction of 0.3 is only incidentally rational in the rather strange ten-base summed exponential string case, but it is not rational when expressed using any other summed exponential string base number. Do modern number theorists, who make a great distinction between rational and irrational numbers know what they are talking about? Absolutely not.

Are people numerate, even if they are not officially licenced as card carrying members of the cult of neo-Pythagorean numerical witch doctors? I would say that in spite of attempts by the said cult to confuse them, non-members of the cult are virtually all completely numerate. For example, if I explained that £100,000 is one thousand times more than £100, which is one thousand times times more than 10 pence, I do not think that anybody could have lost my thread yet. I must explain here that there are two kinds of pounds, the gold-pound (£g) and the imaginary pound (£f). Without this very simple concept of an absolute pound, any attempt at understanding the mathematical science of money is doomed to failure. There is a physical representation of a gold- pound and that is the Royal Mint gold sovereign, which still has a nominal face value of one pound. Prior to WW1, this coin was quite simply one pound. This nice little coin is still minted by the Royal Mint today and one can still easily exchange gold pounds for imaginary pounds and visa versa, through any one of a very large number of global dealers.

If you changed say £100,000 into gold pounds today, they would hand you about 171 one pound coins. If you immediately wanted your imaginary pounds back, you would get back say £98,000. These are two different money systems. Try changing your electronic pounds into US$ and then change back again and you will experience a loss on the double conversion, the dealers have to live. The loss on the double conversion is only so high (2%) with the physical gold pound because the coins cannot be transferred electronically. It is far worse at a cash-note Bureau de Change; at my local Post Office, for the £-Euro-£ round trip conversion in cash notes, there would be about a 15% loss on the double conversion.
 
There is no physical representation of the modern imaginary pound. There are still physical bank notes but those are just paper vouchers for imaginary pounds, with token coins for the fractions of £5. In 2001, shortly before I decided to take up quantum physics, I bought a few gold sovereigns. At the time, the price of the coins was about £55 each. Over the last 24 years, the imaginary pound has so lost its credibility that one must now pay or receive about 580 imaginary pounds in exchange for a single real pound.

In this example, the loss of purchasing power of the imaginary pound over the last 24 years is about 10.5 times. Using exponential arithmetic, I can easily find the average value depreciation rate as being the 24th root of 10.5. I just need to find 10.5^(1/24) which is about 1.103. The smoothed average exponential value decay rate has been 1/1.103 times per year, that is a 9.4% compounding loss in real value for every year since 2001. The half-life of the imaginary pound in the 21st century is given by log(2)/log(1.103) = 7.07 years. Should any sensible real-value saver buy UK government bonds yielding less than 12%? Absolutely not. So, why does your pension fund buy these bonds? They are not stupid, pension law obliges them to.

What about the fractional ratios of ten, how numerate are we with those?
Well, we are all capable of this numeracy with the fractional ratios of ten, but only if we know our times tables. In 1975, I was sat in a top engineering office in Frankfurt Am Main talking to one of their very best engineers, a man who was fluent in five European languages and was paid the today equivalent of about Euro 900,000 per year. As one would expect of course, he drove about in an almost new Porsche. He said in German “now let me see, that would be 0.6 times 7”. He reached for his calculator but before he could start, I said in German “four point two”. He fiddled with his calculator to find that the answer was indeed 4.2. Once he found that I was right, he looked at me as if I was some strange alien genius who had just walked off my space-ship. Despite his high status and double doctorate in engineering, that man was pathetically innumerate. If one does not know what 0.6 x 7 means, then what on earth does 4.2 mean?

There is a simpler way to deal with the fractional ratios of ten.
Over 400-years ago, John Napier told us all about this simpler way. We need to think of our ratio-metric numerical values as existing upon an exponential scale. When I was young and foolish (as opposed to my being old and foolish today), I used a tiny sum of money from businesses that I was running while only pretending to be a university student of electronic engineering, to buy a very nice German-made Faber Castel slide rule. This was only a status symbol, just like that man’s Porsche, but not so expensive. I still have it today, 52 years on and never used. Why did I even bother with university at all? It was the grant money and the free “education” you see. In those days, just so long as one never bothered to waste one’s time and actually go in, the “cost” of the four year course was about the equivalent today of getting a
£50,000 tax free handout for nothing. They paid me to pretend to study under them and in return for that, I pretended to learn from them. It was a system that worked really well for me, it is called Communism.

In the UK today, those happy memories of our glorious Communist past are now long gone. Despite borrowing about 9% of GDP at hyper-negative real rates of interest, collecting about 37% of GDP in taxes, a rate taking them beyond the Laffer peak, and cooking the books far better than Enron ever did, HMG can no longer even afford to plug the pot-holes in the roads, let alone the sheer luxury of Communism.

About three years after I bought the slide rule, I bought a magnificent Sharp calculator that could do everything; hex, octal, decimal, binary and natural expressions of numbers and with its 48 character by two line alphanumeric display, I could add any personal private calculation that I wanted to using the BASIC programming language. My programs were stored in a large memory. As I remember it, the device sported a dozen or so user defined keys to which one could attach any one of one’s private programs. The Japanese instruction manual was an utter masterpiece. For example, if one wanted to know how to calculate the natural logarithm, they did not hold back on how to do this. From their explanation, I programmed a private key to give the natural logarithm, and bingo my private key gave exactly the same answer as the public natural logarithm (ln) key that they provided as a standard preset.

Why do people find the language of numbers so confusing?

With any logarithm of any base, we do not write out a series of summed exponential strings as we have to do with a flat (finger counting) number. We simply introduce a higher number that is the exponent of a base number. To help explain this, I will give a simple example here. Let us take the flat (finger counting) number expressed in decimals as 65,536. In this example, we will use the simple two-base exponential. I want to find the 2-base logarithm of 65,536, the answer here is just sixteen; 2^16 = 65,536. The two is the exponential base, the 16 is the exponential number and the 65,536 is the flat finger counting number. If presented with a flat finger counting number (that is the 65,536 number in my example), Napier showed us how to calculate the exponential number (the 16 number in my example) for any base value, not just for 2 or 10.

It always beat me why people found all this so confusing, until that is, I realised that they were calling the exponential number the logarithm. That word “logarithm” is in Elizabethan (Shakespearean) English. Napier chose the name “logarithm” in an era when most polite educated people only spoke about serious academic subjects to each other in Latin. He published the work before the original King James Bible first went to press in 1611.

Are people actually confused about mathematical transforms or are they merely pulling my leg?
Have you ever heard about mathematical transforms? Even if this is all Greek to you, you use mathematical transforms all the time without even knowing about it. How do I encrypt the sound waves of your voice into digital binary numbers flying down the fibre optic pipe? I could use a simple 16 bit analogue to digital conversion of the sound waves of your voice and try sending those. I would only do that if I was a brain dead neo-Pythagorean number theorist, but fortunately I am not one of those. Instead I use a modified Fourier Transform of the wave form numbers. I do this because it takes up perhaps as much as 10 times less communication bandwidth.

The first and very simplest mathematical transform ever found was the exponential transform into the exponential numerical domain and the reverse exponential transform back into the flat finger counting numerical domain. Other names for the exponential domain could be the multiplicative domain or the domain of human numeracy. These two complimentary mathematical transforms were both published by John Napier over 400 years ago. Just because 430 years ago Napier called the forward exponential transform the logarithm and the reverse exponential transform the anti-logarithm, that is no excuse for not understanding these two vital exponential numerical domain transformations today. This is especially true because in 1970, before those modern numerical witch doctors set the clock back by 450 years with all of their deranged claptrap, I can hardly have explained anything yet that was not taught to smart 13 year old children in 1963.

Napier and Euler, two of the six greatest mathematicians of all time.
Just one of Napier’s many great achievements was to show us the natural exponential constant. For this he makes the exponential base the very base of mother nature herself, it is about 2.718 and Napier (bless him) worked this out for us to about 10 significant digits. Over one hundred years later, Leonard Euler called this constant “e” and showed its value to be the sum of an endless converging series. Did Euler add any real value to Napier’s work? In my opinion, absolutely not. But to try and work out which great mathematician added the most value overall, I would first need to ask Leonard Euler what he was smoking because the work that he left lying around unfinished for me to just pick up and complete for him, was no more than a few minutes of mild pleasant effort for me at age 13 in 1964.

It is like the most intuitive geological miner of all time spent his entire life digging for a great mother load of value that he knew must be there, but walked away in the end with almost nothing to show for it, leaving a vast great empty gaping hole in the ground. Then two hundred and thirty years later, a know nothing 13 year old boy whose only real interest was in dating older girls and riding bikes and who loathed all mining activity, sauntered into the old mine out of mild curiosity, wiped a thin layer of rubble from the working face where the great miner had left off, instantly revealing Euler’s mother load in all its glory.

Leonard Euler gave us his famous Identity, there was only one problem, he clearly had no concept of exponential polarity. The units of rotational polarity on the flat numerical plane are quite clearly the quadrant, not the radian; and Leonard, where is your exponential magnitude?

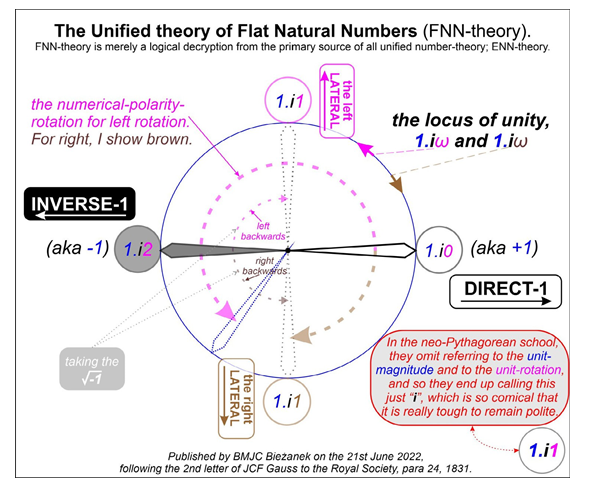
From the above shown interpretive quantum leap, it is a simple matter to draw a circle of unit radius, which we can call the circle of unity. The centre of our circle must be placed at the absolute numerical vanishing point where the magnitude of the radius vanishes entirely. This circle can be thought of as connecting all the possible directions in which a unit vector can point upon a two
 
dimensional number plane. We then merely allocate the number direct-one (aka +1) to one point on the circle. This is shown conventionally in my following sketch. The number inverse-one (-1) then automatically pops up on the opposite side of the circle to direct-one (+1) as shown below.

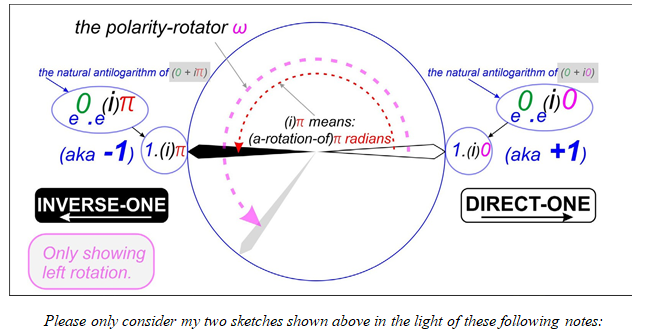
1)    The (i) operator means “a-rotation-of”, it MUST be followed by a numerator, typically one quadrant of rotation. On its own, the (i) operator is arithmetically meaningless. Mathematicians do write
(i) on its own with no polarising numerator, for example 123(i)
{instead of 123.(i)1 }, when they do that they are missing out the times dot and the unit numerator, which seems to their naive and gullible minds to make no difference at all. Well, good luck with that one.

2)    The natural antilogarithm of iπ (that is e^iπ) is simply iπ. In other words; the polarity-rotation is indifferent to the use of the exponential or the flat numerical form of the magnitude. We should not be using radians as our unit of polarising rotational angle at all, but nevertheless, where we do this, this remark must apply. In general, e^iω = iω for all finite ω, where ω is a polarity rotation in quadrants units.

3)    The number (0 + iω) is a valid and complete exponential number. On its own, zero in the exponential domain implies a unit magnitude but of no polarity and iω on its own implies a polarity rotation of ω quadrants but of no magnitude. Neither of the two parts of the exponential number (0 + iω) have any arithmetical meaning on their own, the exponential number (0 + iω) only acquires an arithmetical meaning when it is stated in full.

8.    Why is understanding natural exponential arithmetic so important?
Anybody who is never concerned with the numerical modelling of cyclically repeating data in a time series can just go back to sleep here and forget all about this issue. However, in quantum physics
 
and in electrical engineering (never mind with astrophysics) ignoring the potential of natural exponential arithmetic is quite out of the question. At first glance, the natural exponential numerical domain and the flat numerical domain seem to be merely giving us two alternative numerical views of the same numerical thing. That is indeed true, but only from a single or fractional rotational cycle perspective. The natural complex exponential number plane can effortlessly show unlimited rotation of not only more than one single cycle of polarity rotation, but even an infinite extent of repeated rotational cycles.

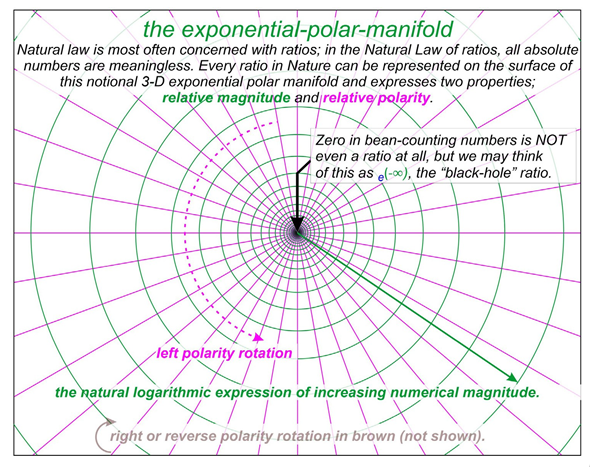
In order to get onboard with the natural exponential numerical domain, we can first examine the Exponential Polar Manifold. This manifold is merely a transitional device that empowers our exponential numerical thinking. The manifold is an infinitely thin membrane which must be seen in three dimensions. We use this 3D manifold to understand the relationship between the exponential numerical domain of Nature and the flat complex numerical plane of our King Canute fans, our post-1972 neo-Pythagoreans, but only for a single cycle of rotation.

The shape of the manifold is reminiscent of an old fashioned long straight trumpet. Imagine that the “trumpet” is in a stand that holds it upright with the sound outlet horn pointing upwards. My first view of the Exponential Polar Manifold is the view looking down into the “trumpet’s horn” from above and from slightly inside the horn and with the infinite realms of the wider horn stretching out exponentially and infinitely about us as it climbs linearly up above our downward facing gaze.

My second view of the exponential polar manifold is of a sectional side elevation of it. As the manifold has absolute rotational symmetry about the vertical axis, the actual angular plane of this vertical section shown here is arbitrary

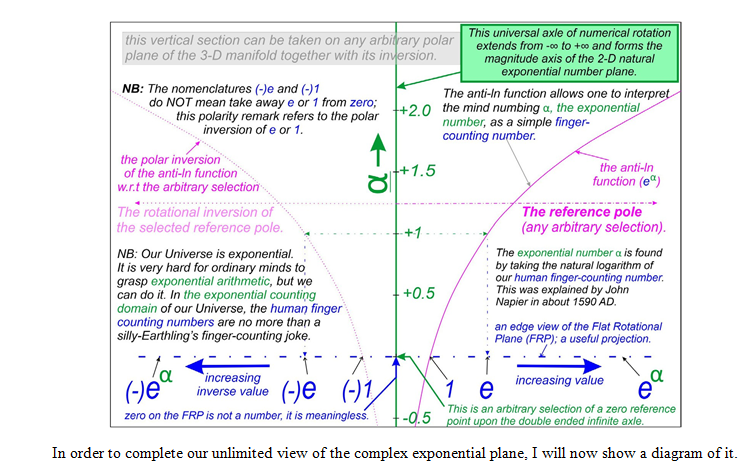
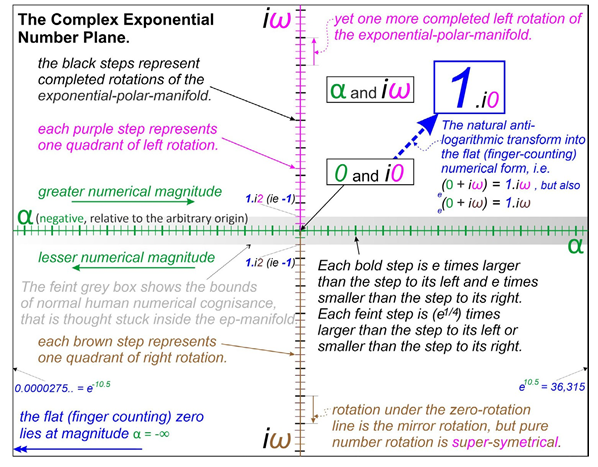
A simple derivative of the inner core of the complex exponential number plane is formed from a flat horizontal section of that transitional exponential polar manifold, taken on the α = zero plane. This view of numbers should not be called the complex number plane at all, but rather the flat rotational plane (FRP).

Conclusion

Unfortunately, ever since about 1972, all mathematics students, including the next generation of university maths teachers, have all been accidentally hypnotised by the action of well-meaning social education science reformers of maths education into learning a lot of utterly puerile nonsense and not even noticing what a bad arithmetical place it was that they had all been taken into. Rather than search for answers and look for where they had all been led astray, the generation of university maths teachers from the class of 1972 decided to join a tiny clique holding on to ideas disgraced over 1,900 years ago and turn themselves back into a cult of neo- Pythagorean numerical witch doctors. Well, as the saying goes, “the devil makes work for idle hands”. Bring back our practical applied mathematicians and leave those neo-Pythagorean numerical witch doctors to stew in their own juice. Cut off their oil and water, de- fund the lot of them.

I would remind readers that we all live out our very short lives on the tiny useful land surface of a tiny piece of the flotsam and jetsam in solar orbit. The Earth is merely 3 parts per million of the system total mass, so think of the Earth as just a rather strange tiny piece of flotsam in comparison to the Sun. For the most recent 60 solar orbits since 1965, theoretical astrophysicists, employing the most powerful numerical models possible with the latest generation of supercomputers, are no nearer to explaining how a single stellar object in the entire Cosmos ever forms in the first place, than they were in 1730. Well, perhaps if they studied my latest work they could at least find that their former numerical impotence had quite simply gone away. My 2015 book “Mass Compaction Mechanics” would probably be beyond them, but where there is life there is hope.

Footnote 1: The Exponential Solution (to Einstein's field equa- tions).

In flat counting (or finger counting), rotation is not expressed as an integral part of a number, although this is inherent in the pi radians of relative rotation implied between direct (positive) numbers and inverse (negative) numbers. However, in the exponential numerical domain, the full two dimensional polarising rotational gamut of the magnitude ratio is expressed within the two dimensional exponential number itself. In order to solve for the field equations of Einstein's General Theory, while maintaining a solution fitting in with the logic of special relativity, we find ourselves only able to express the General Theory solution in the natural exponential numerical domain. There is no solution in the flat (finger counting) numerical domain that is even possible. As I have found that people are rather confused about these simple basic issues, I have given, within the above essay, an overview of all of our arithmetic and of our largely misunderstood codes for the various forms of numerical expression. By the way, the special theory partial solution turns out to be trivial, this partial solution for the special case only retains her meaning while the inertial mass is expressed in energy equivalent units;

Technical Appendix

c^2 = -1