Research Article - (2025) Volume 8, Issue 1
The Relativistic Big-Bang and the Thermodynamic Importance of Initial Cosmic Kinetic Masses
Received Date: Jan 03, 2025 / Accepted Date: Feb 10, 2025 / Published Date: Feb 14, 2025
Copyright: ©2025 Hans J. Fahr. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation: Fahr, H. J. (2025). The Relativistic Big-Bang and the Thermodynamic Importance of Initial Cosmic Kinetic Masses. Adv Theo Comp Phy, 8(1), 01-06.
Abstract
In recent papers by Fahr (2023) and Fahr and Heyl (2024) we had shown that an instantaneous, initial Big-Bang explosion of a purely material universe can not have happened [1,2]. At least not by itself, as is most often envisioned, any way not solely caused by the enormous pressure of the matter in the singularity of the initially extremely hot, highly condensed cosmic matter.
This is due to the strongly enhanced centripetal gravity field, increased by the gravitating mass of the relativistic, kinetic cosmic masses. where by the anticipated explosive action of the material pressure is nullified. Instead, as was argued by us, the initial "Bang" rather must have started from a pressurized cosmic vacuum with its explosive pressure, otherwise a "Bang" never could have happened.
In the above mentioned papers we thus analysed how to adequately describe this cosmic vacuum pressure and how to formulate the initial scale expansion of the universe, occuring solely on the basis of that newly considered, cosmic ingredient. Thereby it became evident that for a needed positive vacuum pressure the thermodynamic polytrope relation between vacuum energy density ρvac and vacuum pressure pvac for the purpose of a cosmic scale expansion �? > 0 only allows for a very limited range of vacuum polytrope indices ξ of 3 < ξvac < 5. For the prefered value ξvac = 4, one can derive a complete description of the cosmic vacuum energy as function of the cosmic scale R and the cosmic time t with inclusion of a process of cosmic matter generation in the course of the cosmic expansion by a specific vacuum condensation process producing a material universe for the later expansion phases. As result one so far obtains a matter universe well familiar to all present day astronomers, however, without the need for an initial, purely material Big-Bang of a mass singularity.
The aspect which was not carefully taken into account so far is the cosmologic importance of the initially relativistically hot cosmic matter and its genuine thermodynamics. This shall become the new subject here. As a surprise, however, in any case the Hubble expansion of the post-recombination universe under the action of cosmic vacuum pressure drives the baryonic distribution function into a more and more non-equilibrium shape with over-Maxwellian populations of the high velocity wings demonstrating surprisingly enough that the cosmic matter temperatures in this expansion phase are in fact increasing with scale R, opposite to classical expectations which, strictly speaking, would predict adiabatic temperature decreases. We determine the distribution function of cosmic gases in this expansion phase and find that structure formation must have run different from what is presently thought.
Keywords
Big-Bang Cosmogony, Cosmic Vacuum Energy, Relativistic Gas Pressures
Introduction
Even the Hottest Cosmic Matter would not explode by itself!
We had shown in recent publications that an initial explosion of the virgin universe can at least not have happened simply by a highly pressurized cosmic matter singularity [1,2]. This is because of the appearance of an unavoidable, extremely strong centripetal gravitational field in connection with a highly concentrated and extremely heated central mass singularity. This holds even though the natural centripetal material pressures have to be taken into account which under these conditions certainly are enormous and definitely would somehow enter the cosmic game. But since the extremely hot cosmic matter has relativistic temperatures, this also leads to relativistically enhanced gravitating mass sources m = m(v → c) > >m0, and thus to even stronger centripetal gravitational fields connected with them. That may at first glance appear controvisionary, but as could already clearly be seen from the two cosmologic Friedman equations [3,4]:

with R = cosmic scale; k = curvature parameter; Λ = vacuum energy density; p = material pressure; ÃÃÂ?µ material energy density, describing the cosmic scale R as function of the cosmic time t, it becomes evident that with vanishing curvature k = 0 and vanishing vacuum energy, i.e. with Λ = 0, the second Friedman equation attains the form
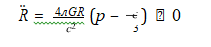
which, perhaps as a surprise, shows that the relativistically hot, enhanced cosmic matter with ÃÃÂ?µ ≥ p strengthens the centripetal gravity field such that no explosive cosmic motion, but just the opposite - "an implosion" - would be caused. The hotter the matter (i.e.ÃÃÂ?µ > p) is in the mass singularity, the more the situation thus resembles that of a singular "black hole". The remaining question only is: What exactly is the energy density ÃÃÃÃÃÃÂ?????ÂÃÃÃÃÂ????ÂÃÃÃÂ???ÂÃÃÂ??ÂÃÂ?µ of relativistically hot cosmic matter?
Relativistically Enhanced Cosmic Masses
Let us start here looking at the mass of a cosmic particle with rest mass m0 which is accelerated by cosmic forces, like thermodynamic ones or gravitational ones, to higher velocities, i.e. towards v ~ c. How then is its dynamic and gravitating mass m = m(v) changing under these circumstances? And how is this then changing the cosmic dynamics?First it turns out that the relativistic mass of this particle is given by [5]:
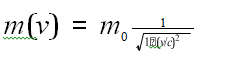
clearly expressing that for v → c its mass m(v) is growing to infinity, meaning that forces further will not accelerate this mass, but only increase its mass. If, however, all the relativistic, dynamic cosmic masses m(v) in this phase of the cosmic expansion determine the cosmic gravity field, then it simply means that cosmic gravity correspondingly is enormously enhanced under these conditions, and with ÃÃÂ?µ increasing under such conditions the explosion is unavoidably inverted into an implosion, as already the second of Friedman‘s 
As shown by Fahr (2022, 2023) only a medium that can realize a cosmic pressure without an initial singularity of relativistically hot matter can cause an initial explosion of the universe; this namely is the recently more and more discussed, cosmic vacuum energy vac connected with a specific, positive vacuum pressure pvac as we may demonstrate and specify further down here [6].
Controle on Relativistic Cosmic Particles
In an earlier paper we had shown how to make sure that the cosmic distribution function does not allow for superluminal particles, and as well that the moments of this distribution function do not contain irrealistic contributions from such non-existing superluminals [7]. The recipe for that not to happen was to write the distribution function as function of the kinetic particle energy Ekin and to find for instance in the case of a prevailing kappa-function fK(v) for the gas particles in the collision-free phase of the cosmic expansion with v ? kc ? H= kc v (R? /R) with λc as mean free path with respect to collisions, and H as Hubble constant (see Fahr, 2024) according to French (1968) with [8,5]:

showing that at the velocity v = c the distribution function drops to zero, i.e. fK(v = c) = 0, and the differential energy density shown in Figure 1 also drops down to ÃÃÃÃÂ???ÂÃÃÂ??ÂÃÂ?µ(v = c) = 0.
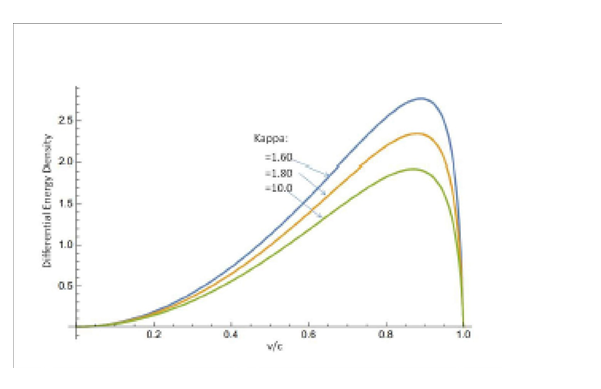
Figure 1: Shown is the Differential Energy Density ÃÃÂ?µ= ÃÃÂ?µ(v/c) As Function of the Upper Velocity in Units of (v/c) for Different Values of Kappa = 1.6; 1,8; 10.0
The Big-Bang Starts from a Pressurized Cosmic Vacuum
Perhaps the best explanation of the problematic begin of our universe would be to assume that this universe does not at all start from a matter singularity, but rather from a vacuum singularity with no initial matter involved at the beginning of cosmic time t → 0.
The latter, however, is systematically generated in the course of cosmic time t, when the metric of the universe is expanded connected with the conversion of vacuum energy into matter energy. The concept of a pressurized cosmic vacuum doing this job at this physical event has to start from the unavoidable thermodynamic condition that energy needs to be consumed in order to cause a blow-up of the universe. This means the fact has to be respected that the action of the cosmic vacuum pressure pvac, i.e., the positive work that has been carried out for blowing up the volume of a spherically symmetric universe, requires a loss of vacuum energy density ÃÃÂ?µvac when causing this change.
This prerequisite is fulfilled, if the following, well known thermodynamic relation holds [6]:
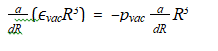
where R is the radial scale of the universe. As shown by Fahr (2023) this relation is mathematically satisfied, if the following polytropic relation is valid between the energy density ÃÃÂ?µvac and the pressure pvac of the cosmic vacuum pvac = -(3 – ξ) ÃÃÂ?µ3. Hereby ξ is the so-called, presently unknown vacuum polytrope index ξ = ξvac [1]. The exact value of the corresponding number ξ = ξvac, however, is presently not known or physically prescribed. The range of permitted values can, however, be strongly reduced. Namely for a non-vanishing, positive cosmic vacuum pressure, needed to physically explain the initial expansion of the universe, it is at least required that the following relation holds pvac = -(3 – ξ)ÃÃÂ?µvac /3 ≥ 0. For a positive vacuum energy and a positive vacuum pressure it is thus required that ξvac ÃÃÂ?µ3. A positive vacuum pressure at this place must be requested in analogy to the thermodynamic pressure since expressing the mean kinetic energy, i.e. a positive moment of the distribution function f(v) [9,10]. Furthermore one can derive in addition from the second Friedman equation for an initially expanding universe with R as its radial scale and R? = d2R/dt2 > 0 the result [1]:

The Matter Temperature in the Vacuum-Driven Hubble Universe
Starting from the first of Friedman´s differential equations which can be given in the following form [1]:

finds the relation between cosmic scale and cosmic time in the compact form:
X2 = 2Y - 1. This relation defines for the given conditions after the recombination of baryonic matter, how the scale R and the time t of the universe are furtheron related to eachother
Thermodynamics under Cosmic Vacuum Action
In an earlier gas kinetic analysis of the cosmic baryon gas behaviour in a vacuum-driven universe expansion after the time of recombination by Fahr (2021) it had been shown that (see Figure 3 there) that the gas temperature during the expansion of the gas over 1, 2, 3, 4, Gigayears - instead of adiabatically decreasing - in fact does increase by a total factor of 1.8 [13]. This is due to upcoming conversion of the initial Maxwell-Boltzmann baryon distribution into an increasingly non-Maxwellian NLTE distribution with over-Maxwellian high velocity wing populations. This latter phenomenon is due to the expansion of the universe by the action of the vacuum pressure, instead of by the action of the thermal pressure!
One might want to see this result compared to the normal gas dynamic case, when the thermal pressure is responsible and drives instead an adiabatic expansion. In the latter case temperatures instead should have decreased, namely according to the following Poissonian relation:


Conclusion
We have shown in this paper above that the initial explosion of the universe cannot be caused by a singularity of overdense, hot cosmic matter, because in that case the overdense matter would have to be extremely hot and highly relativistic. This would, however, just strengthen the centripetal gravity field such that an expansion of the universe along this way would be impeded which is also clearly reflected by the two Friedman differential equations. As we show here, an initial centrifugal, explosive event of the universe can only cosmically and physically be caused by a pressurized cosmic vacuum with properties that we have derived above as function of the scale R and time t of the universe. However, for that to become true, one first had to clarify how the structure formation in the universe in the post-recombination period can be caused under increasing NLTE matter temperatures. We can show that a conversion process converting vacuum energy into quantized massive matter can be discussed which explains why at present times we find a partially materializeduniverse, however, why this universe contains stars, galaxies and clusters of galaxies which can be observed by mankind - , and what are the final consequences of the ongoing vacuum energy decay at the ongoing expansion of the universe - that ahead of all must be clarified at first [12,16-18].
References
1. J Fahr, H. (2023). The cosmic big-bang: how could mankind escape from it?. Physics & Astronomy International Journal, 7(1), 74-75.
2. Fahr, H. J., Heyl, M. (2024). The Cosmic Vacuum Pressure Polytrope: What Causes the Big-Bang? Adv Theo Comp Phy, 7(3), 01- 03.
3. Friedman, A. (1922). Über die krümmung des raumes. Zeitschrift für Physik, 10(1), 377-386.
4. Friedman, A. (1924). Über die Möglichkeit eienr Welt mit konstanter nagativen Krümmung ders Raumes, Zeitschr. f. Phys, 10(21), p326.
5. French, A. P. (1968). Special relativity. Massachusetts Institute of Technology.
6. J Fahr, H. (2022). Cosmic vacuum energy with thermodynamic and gravodynamic action power. Physics & Astronomy International Journal, 6(2), 62-66.
7. Fahr, H. J., & Heyl, M. (2020). Suprathermal plasma distribution functions with relativistic cut-offs. Monthly Notices of the Royal Astronomical Society, 491(3), 3967-3973.
8. Fahr, H. J. (2024). Is the Evolution of Mankind and the Universe Solely a Physical Selfrunner? Adv Theo Comp Phy, 7(4), 01-08.
9. Chapman, S., & Cowling, T. G. (1990). The mathematical theory of non-uniform gases: an account of the kinetic theory of viscosity, thermal conduction and diffusion in gases. Cambridge university press.
10. Cercignani, C. (1988). Kinetic Theory of Gas Dynamics and the Boltzmann equation, Springer.
11. Farnes, J. S. (2018). A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. Astronomy & Astrophysics, 620, A92.
12. Arghirescu, M. (2015). The Cold Genesis of Matter and Fields. Science PG, 4(2).
13. Fahr, H. (2021). The baryon distribution function in the expanding universe after the recombination era. Physics & Astronomy International Journal, 5(2), 37-41.
14. Gerthsen, C. (1958). Lehrbuch der Physik, Springer Verlag, Heidelberg.
15. Fahr, H. J., & Willerding, E. (1998). Die Entstehung von Sonnensystemen: eine Einführung in das Problem der Planetenentstehung. Spektrum, Akad. Verlag.
16. Robertson, H. P. (1933). Relativistic cosmology. Reviews of modern Physics, 5(1), 62.
17. Einstein, A. (1917). Kosmologische betrachtungen zur allgemeinen relativitätstheorie. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 142-152.
18. Fahr, H. J., & Heyl, M. (2007). Cosmic vacuum energy decay and creation of cosmic matter. Naturwissenschaften, 94, 709-724.