Introduction

Large Language Models (LLMs) have emerged as transformative tools in natural language processing, demonstrating remarkable capabilities in tasks ranging from text generation and translation to question answering and code completion. At the heart of these models lies a sophisticated mechanism for representing text: high- dimensional vector embeddings. These embeddings map words, phrases, and even entire documents into a continuous semantic space, where geometric relationships reflect semantic similarities. For instance, words with related meanings are positioned closer together, while dissimilar concepts are further apart.

While these embedding spaces are often treated as continuous for practical purposes, a fundamental aspect of LLMs hints at an underlying discreteness: their reliance on a finite vocabulary of tokens. This discrete foundation suggests that the seemingly continuous semantic space might, in fact, possess a quantized structure, analogous to the discrete energy levels observed in quantum systems. This inherent quantization prompts a compelling question: can we leverage the powerful theoretical frameworks of mathematical physics and tools of quantum mechanics to gain a deeper understanding of the organization and dynamics of these semantic spaces? Furthermore, if this quantization is valid, could quantum computing, for example, offer new approaches to training or exploiting these models, potentially unlocking significant performance gains?

This article embarks on an exploration of this intriguing analogy between LLM embedding spaces and quantum mechanics. We focus on the concept of quantization, the wave-like behavior of semantic representations, and the potential for quantum-like models to illuminate the inner workings of LLMs. Our central proposition is that the LLM embedding space can be viewed as a quantized semantic space, where individual words and phrases correspond to distinct quantum states. This perspective allows us to draw parallels between the probabilistic outputs of LLMs and the inherent uncertainties characteristic of quantum systems.

A key element of our approach is the extension of the standard, real-valued embedding space to the complex domain. This complexification enables us to model semantic interference effects, drawing direct parallels to phenomena such as the double-slit experiment in quantum mechanics. We demonstrate how this complex representation, combined with concepts like potential landscapes (e.g., the double-well potential for modeling semantic ambiguity) and path integral formalisms, can provide new insights into the behavior of LLMs, including their ability to generate creative text and handle nuanced semantic relationships.

By embracing this interdisciplinary approach, we aim to establish a theoretical foundation for understanding LLM behavior through the lens of quantum mechanics. We propose that LLM embedding spaces exhibit emergent properties analogous to quantum systems, potentially leading to new views in natural language understanding and generation.

Background and Related Work

LLMs have revolutionized Natural Language Processing (NLP), achieving state-of-the-art results in various tasks such as text generation, translation, and question answering. These models are typically based on the Transformer architecture, which utilizes self-attention mechanisms to capture long-range dependencies in text [1]. A key distinction of the Transformer architecture is its departure from previous recurrent neural network approaches. Instead of recurrence, the Transformer relies entirely on attention mechanisms, enabling parallel processing of the input sequence and significantly improved training efficiency. The Transformer architecture has enabled LLMs to scale to unprecedented sizes, with models like BERT and GPT-3 containing billions of parameters [2, 3]. The self-attention mechanism is a core innovation of the Transformer. It allows the model to weigh the importance of different words in the input sequence when processing each word, effectively capturing contextual relationships. This is achieved by computing attention weights based on the relationships between ”queries”, ”keys”, and ”values” derived from the input embeddings. The attention weights determine the contribution of each word to the representation of other words, allowing the model to focus on the most relevant parts of the input when making predictions. Furthermore, multi-head attention enhances this capability by allowing the model to attend to different aspects of the input in parallel, capturing a richer set of relationships.

A key component of LLMs is the embedding space, where words and phrases are represented as high-dimensional vectors. These embeddings are learned during the training process and capture semantic relationships between words. Words with similar meanings are located closer together in the embedding space, while dissimilar words are further apart. Understanding the structure and properties of these embedding spaces is crucial for interpreting the behavior of LLMs. The geometry of these embedding spaces has been explored by researchers like Mimno and Thompson [4]. Furthermore, the way context influences these embeddings has been investigated by Tenney et al. [5]. Several approaches have been proposed for analyzing LLM embedding spaces. Dimensionality reduction techniques, such as Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE), are often used to visualize the embedding space in lower dimensions [6, 7]. Geometric analysis techniques, such as calculating cosine similarity between vectors, are used to quantify the semantic similarity between words and phrases [8]. These approaches have provided valuable insights into the organization of semantic information in LLMs. Mitchell and Lapata have developed methods for evaluating the compositionality of these models, while Arora et al [9]. have explored the linear algebraic structure of word senses [10].

The connection between information theory and physics has been explored in various contexts. Shannon’s information theory provides a framework for quantifying the amount of information contained in a message [11]. Landauer’s principle establishes a fundamental link between information and thermodynamics, stating that erasing one bit of information requires a minimum amount of energy dissipation [12]. These concepts have been applied to the study of computation, complexity, and the limits of information processing. The application of field theory to classical complex phenomena has also been successful. For example, field theory has been used to model turbulence, providing a theoretical framework for understanding the statistical properties of turbulent flows [13]. Furthermore, field-theoretic approaches are valuable in describing phase transitions in classical statistical mechanics and the emergent behavior of active matter systems [14]. These applications demonstrate the power of field theory to describe emergent phenomena in complex systems.

Our work builds upon these existing approaches by exploring the analogy between LLM embedding spaces and quantum mechanics. Quantum mechanics, pioneered by Heisenberg, Schr¨odinger, and Dirac, provides a powerful framework for understanding the behavior of matter at the atomic and subatomic level [15-18]. Dirac’s work on quantum electrodynamics laid the foundation for quantum field theory, further developed by Schwinger [19-24]. The concept of symmetry, crucial in physics, was formalized by Wigner and plays a key role in understanding particle physics, including the Higgs mechanism [25–29]. We propose a new approach based on quantum principles that leverages the theoretical frameworks of quantum mechanics to gain a deeper understanding of the organization and dynamics of semantic spaces. This approach is inspired by the observation that LLMs rely on a finite vocabulary of tokens, suggesting an underlying discreteness in the seemingly continuous semantic space. We extend the standard, real-valued embedding space to the complex domain to model semantic interference effects, drawing parallels to phenomena such as the double-slit experiment in quantum mechanics. Furthermore, we introduce a new, complex-valued similarity measure that captures both magnitude and phase information, offering a more nuanced comparison of semantic representations. We present a path integral formalism, based on a nonlinear Schr¨odinger equation with a gauge field and Mexican hat potential, for modeling the dynamics of LLM behavior. This builds on previous work exploring quantum- like models in cognition and semantic composition [30-33].

By applying quantum mechanical concepts to the analysis of LLM embedding spaces, our approach aims to provide a fresh perspective on these complex systems. Building on previous work that has explored connections between information theory, physics, and natural language processing, this quantum-like framework has the potential to unlock new understandings of the emergent properties of LLMs and to inspire future research.

 Probabilistic LLM Behavior: The Coin Flipping Analogy 

To begin exploring the analogy between LLMs and quantum mechanics, we first acknowledge the inherent probabilistic nature of LLM outputs. While often perceived as deterministic systems trained to mimic human language, LLMs exhibit a degree of randomness, particularly evident in text generationThis stochasticity arises from the sampling process used to select the next token in a sequence, where probabilities are assigned to different tokens based on the model’s learned distributionTo illustrate this probabilistic behavior and introduce relevantquantum mechanical concepts, we employ a simple coin-flipping analogy. In the following example, and also in other examples in this article, we use the OpenAI embedding model and gpt-4o. Consider the following prompt presented to an LLM: ”””You are a game machine. Choose a number between 0 and 1. If the number is less than 0.5, enter ”heads”. Otherwise, write ”tails”. Just answer ”heads” or ”tails”.””” When presented with this prompt in a conversational setting (where the history is preserved), the LLM generates a sequence of responses that, over many iterations, approximates a fair coin flip. We observe roughly 50% of the answers being ”heads” and 50% being ”tails.” This empirical observation suggests an underlying probabilistic mechanism governing the LLM’s output, rather than a purely deterministic process. In quantum mechanics, a two-level system provides a fundamental model for describing systems with two distinct and discrete states. Unlike classical systems, a quantum two-level system can exist in a superposition, a linear combination of both states. Familiar examples include the spin of a spin-1/2 particle (spin up or spin down) or the polarization of a photon (horizontal or vertical). The state of a general two-level system can be represented as a vector in a two-dimensional Hilbert space,

|ψ⟩ = c₁ |1⟩ + c₂ |2⟩, (1)

where |1⟩ and |2⟩ represent the two orthonormal basis states, and c₁ and c₂ are complex probability amplitudes. The probability of measuring the system in state |1⟩ is given by |c |², and the probability of measuring the system in state |2⟩ is given by |c |². These probabilities must sum to one, reflecting the certainty that the system is in one of the two possible states upon measurement.

|c₁|² + |c₂|² = 1.              (2)

We can draw a conceptual analogy between the LLM coin-flipping example and a quantum two-level system. Let |heads⟩ and |tails⟩ represent the two possible states of the LLM’s response, analogous to the spin-up and spin-down states of a spin-1/2 particle. The prompt can be viewed as an ”interaction” or ”measurement” that forces the LLM to ”choose” between these two states. Prior to theprompt, the LLM can be considered to be in a superposition of these two states,

|prompt⟩ = c₁|heads⟩ + c₂|tails⟩.                      (3)

In this analogy, c1 and c2 represent the probability amplitudes for the LLM to respond with ”heads” or ”tails”, respectively. The observed frequencies of ”heads” and ”tails” in the LLM’s output can then be interpreted as the probabilities of measuring the system in each state,

|⟨heads | prompt⟩|² ≈ 0.5  (4)
|⟨tails | prompt⟩|² ≈ 0.5 (5)

While this analogy provides a useful and intuitive starting point for understanding the probabilistic nature of LLMs, it is crucial to recognize its inherent limitations. In the quantum mechanical example, |heads⟩ and |tails⟩ represent distinct and orthogonal quantum states, not simply vectors in a real-valued embedding space. Furthermore, the dynamics of a quantum system are governed by the Schr¨odinger equation, which describes the evolution of the wave function and the superposition of states. The act of measurement in quantum mechanics also leads to the collapse of the wave function into a single, definite state. These concepts are not directly mirrored in the standard LLM architecture. Furthermore, the standard LLM embedding space does not inherently support complex probability amplitudes, which are essential for describing quantum interference effects. These limitations motivate the need for a more sophisticated model that can capture the wave-like behavior of semantic representations and incorporate complex phases, as we will explore in the following sections.

Core Quantum Mechanical Analogies
It is crucial to first clarify the role of nonlinearity in the context of LLM embedding spaces. We distinguish between two key stages:
(1) the LLM’s training process and prediction calculation, which are inherently nonlinear due to the use of neural networks with nonlinear activation functions, and (2) the subsequent analysis of the learned embeddings, such as calculating cosine similarity between vectors. While the latter is a linear operation, it operates on vectors resulting from a nonlinear process, thus inheriting the effects of that nonlinearity. Based on this distinction, we will explore two complementary approaches in this article: one that leverages the linearity of the embedding space when comparing results (embedding vectors, states) and another that explicitly incorporates nonlinearity during result calculation to capture morenuanced semantic phenomena.

To draw parallels with quantum mechanics, we adopt the following key assumptions:
1.    Completeness of Vocabulary: We assume that the LLM’s finite vocabulary forms a (approximately) complete basis for representing semantic information. While this is not strictly true, we treat it as a reasonable approximation for the purposes of our analogy.
2.    Semantic Space: Drawing an analogy to quantum mechanical
phase space, we define a semantic space as the complex extension of the embedding space (or, equivalently, the configuration space). If the embedding space has dimension N, the semantic space has 2N real dimensions. This doubling of dimensionality arises from the complex extension, which effectively provides 2 degrees of freedom for each original dimension in the configuration space. This allows the modeling of interference effects and other quantum-like phenomena within the semantic space. Analogous to how time is treated in classical mechanics, the time taken for an LLM to generate a prediction from a given input is considered separately from the semantic space itself. While phase space describes the possible states of a system at a given time, and time evolution traces a trajectory through phase space, the ’time’ dimension for LLM prediction generation is not included as a dimension within the semantic space. It is a parameter that governs the evolution or trajectory through the semantic space.
3.    Quantized Semantic States: Semantic states are discrete and distinct, analogous to the quantization of energy levels in quantum systems. This allows us to represent words and phrases as distinct quantum states within the semantic space. The reliance of LLMs on a finite vocabulary of tokens provides a basis for this assumption, suggesting an underlying discreteness in their semantic processing.
4.    Schr¨odinger Equation for Semantic Wave Propagation (Linear Model): In our first approach, we treat the semantic space as linear. The evolution of the semantic wave function within this space is governed by the standard, linear Schr¨odinger equation. This equation serves as a fundamental description of wave propagation for non-relativistic particles in the absence of explicit nonlinear effects. This approximation is valid when considering basic semantic relationships and allows us to leverage the superposition principle and plane wave solutions.
5.    Nonlinear Semantic Wave Propagation (Nonlinear Model): In our second, more sophisticated approach, we explicitly account for the nonlinear nature of the embedding space. We model this nonlinearity through two distinct mechanisms: (a) by introducing a cubic term directly into the Schr¨odinger equation, resulting in a nonlinear Schr¨odinger equation (NLSE), and (b) by employing nonlinear potential functions. The cubic term allows us to explore phenomena such as semantic self-interaction and the formation of semantic solitons. Nonlinear potentials, such as the double-well expansion in terms of basis states. The interaction between semantic charges is mediated by the gauge field, analogous to how electromagnetic forces are mediated by photons. Specifically, regions of high semantic charge density attract or repel each other based on the sign of the coupling constant in the nonlinear Schr¨odinger equation or the form of the Mexican hat potential. This interaction influences the overall semantic structure and coherence of the LLM’s representation.

It is essential to emphasize that these are analogies, not literal physical equivalences. They provide a theoretical framework for examining LLM behavior. To manage the computational complexity introduced by nonlinearity in the nonlinear model, we employ approximations when dealing with wave function propagation. It’s important to note that exact solutions to nonlinear equations are rare; therefore, approximations are frequently necessary in these contexts.

Extending the Embedding Space: Semantic Interference and the Need for Complex Representations

The standard LLM embedding space represents words, phrases, and sentences as real-valued vectors. Cosine similarity, a real number between -1 and 1, then quantifies the semantic similarity between these vectors based on the angle between them. While effective, this approach has limitations in capturing more nuanced semantic relationships, particularly those involving contextual information and interference effects. In this section, we propose a theoretical extension where the embedding space is complexified, allowing us to represent ”meaning” as a wave function, where the phase is crucial for capturing interference effects analogous to those observed in quantum mechanics.

Limitations of Real-Valued Embeddings: The Case for Contextual Sensitivity
To illustrate the limitations of the real-valued embedding space and motivate the need for complex representations, consider the task of categorizing LLM entries or distinguishing nuanced differences in word usage. Suppose we want to determine whether a given sentence is related to ”dogs” or ”cats,” or, more subtly, to differentiate between words with similar overall meaning but different contextual appropriateness. We might have the following prompts:
prompt1 = ”I want to talk about cats.”  (6)
prompt2 = ”I like cats.”     (7)
prompt3 = ”I am afraid of dogs.”   (8)
prompt4 = ”Dogs are more loyal than cats.”  (9)

The standard approach is to calculate the cosine similarity between the embedding of each prompt and the embeddings of ”dogs” and ”cats.”

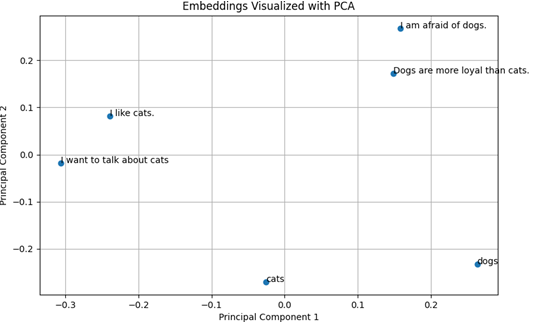
Figure 1: Principal Component Analysis (PCA) projection of word embeddings for ”dogs,” ”cats,” and example prompts. This visualization demonstrates the limitations of real-valued embeddings and cosine similarity in capturing nuanced semantic relationships. While prompts related to ”cats” generally cluster closer to the ”cats” embedding, the overlap between clusters suggests that context and subtle differences in meaning are not fully captured by this approach

Given two vectors A^→ and B^→, their inner product is defined as

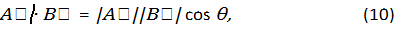
from which we obtain the definition of cosine similarity,

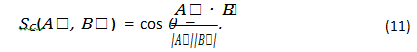
The values are normalized are therefore between -1 to 1. Value 1 corresponds exactly aligned (similar) vector and -1 the most non- similar. In vector embedding space cosine similarity gives a useful measure of how similar two words, sentence or documents are likely to be, in terms of their subject matter, and independently of the length of the documents. Cosine similarity provides a useful measure of semantic similarity, but it only captures the angle between the vectors. It does not account for potential interference effects that might arise from the superposition of different semantic components, nor does it fully capture nuanced differences in word usage. In this example, we might obtain the following cosine similarities:

SC(prompt1,”dogs”) = 0.7924637278190193              (12)

SC(prompt1,”cats”) = 0.8691721116453197               (13)

SC(prompt2,”dogs”) = 0.7948651093796374              (14)

SC(prompt2,”cats”) = 0.8742215747399027               (15)

SC(prompt3,”dogs”) = 0.8292989582958668              (16)

SC(prompt3,”cats”) = 0.7966300696893088               (17)

SC(prompt4,”dogs”) = 0.8295814659291845              (18)

        SC(prompt4,”cats”) = 0.8215583147667265  (19)

We may visualize these embeddings using principal component analysis (PCA), see Figure 1. Semantically similar words and sentencens are closer to each other.

Semantic Interference: Drawing Parallels to the Double- Slit Experiment
To capture potential interference effects within the semantic space of LLMs, we draw an analogy to the double-slit experiment in quantum mechanics, see Figure 2.
In the standard double-slit experiment, particles (e.g., photons or electrons) are directed towards a screen with two slits. The resulting pattern on a detector screen behind the slits exhibits an interference pattern, demonstrating the wave-like nature of the particles. The probability distribution on the screen is not simply the sum of the probabilities from each slit individually; instead, it displays interference fringes due to the superposition of the waves emanating from each slit.
 

The wave functions of the particles passing through each slit can be written as

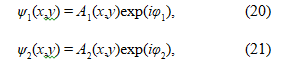
where A₁(x,y) and A₂(x,y) represent the amplitudes, and φ₁ and φ₂ represent the phases of the waves at a point (x,y) on the detector screen. The probability distribution is then given by

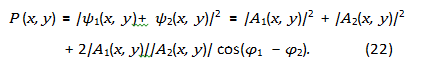
The crucial term 2|A1(x,y)||A2(x,y)|cos(φ1 − φ2) is the ”interference term,” which arises from the superposition of the complex probability amplitudes. A purely real formulation lacks the phase information necessary to describe this interference. The double- slit experiment demonstrates the wave-particle duality of light and matter. Both wave and particle descriptions are valid, and the theoretical framework used to describe the phenomenon depends on the experimental setup.

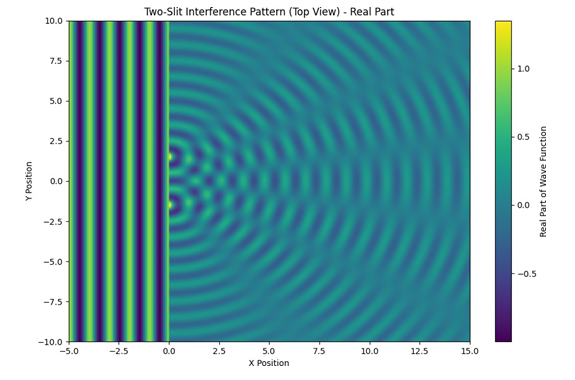
Figure 2: The double-slit experiment, illustrating the importance of phase information in capturing interference effects. In analogy to LLMs, this demonstrates why complex-valued representations are necessary to model the nuanced semantic relationships that cannot be captured by real-valued embeddings alone.

 Extending the Analogy: N-Dimensional Semantic Space
We extend our framework to a higher-dimensional space. Consider an analogous experiment conducted within a phase space of 2N real dimensions, where N represents the dimensionality of the LLM embedding space. An additional dimension represents time. This higher-dimensional space is designed to capture the intricate relationships between semantic concepts. In this analogy, each ”slit” corresponds to a distinct semantic context or a particular facet of a word’s meaning, and the wave function or ”particle” that traverses the slit represents a word, sentence, or paragraph under investigation.

Given that we are currently focusing on the utilization of pre- trained embeddings, rather than the training process itself, we are operating within a regime where the explicit nonlinearities of the training process are not directly considered. Therefore, we treat the semantic space as approximately linear in this context. Consequently, the total field at any point can be approximated as the linear superposition of the individual fields originating from each ”slit.” This allows us to model the semantic wave propagation using plane waves and the principle of superposition.

Under these assumptions, we consider a simplified two-slit scenario where two wave functions, denoted as ψ1 and ψ2, traverse the slits. The total wave function is then given by the superposition

ψ = ψ₁ + ψ₂.                           (23)

Approximating these waves as plane waves, we express them as

where A₁ and A₂ represent the amplitudes, k1 and k2 are the wave vectors in high-dimensional space, ω₁ and ω₂ are the angular frequencies, φ₁ and φ2 are the initial phases. The intensity of the wave function, which can be interpreted as the probability density, is then

This simplified formula provides an approximate means of connecting the intensity (probability of a semantic interpretation) to the cosine similarity between embedding vectors, while also incorporating phase information. The key point is that the phase difference between the semantic waves plays a crucial role in determining the overall intensity, analogous to its role in the double-slit experiment. This suggests that a complex-valued representation, which includes phase, is essential for capturing the nuances of semantic meaning.

The interpretation is similar to the 2D case, but now the interference pattern exists in a much higher-dimensional space. The phase difference φ₁(x) − φ₂(x) captures the relative semantic relationships between the two ”slits” (semantic contexts) at a particular point in the N -dimensional space.

Semantic States as Superpositions: Towards Complex Representations
In the context of LLMs, we can think of different semantic components of a prompt as analogous to the waves emanating from the slits. The overall meaning of the prompt is then determined by the superposition of these semantic components, which can lead to constructive or destructive interference. This motivates us to extend the real-valued LLM embedding space to the complex domain. In this complexified space, each word, phrase, or sentence is represented by a complex vector, and the semantic relationships between them are determined by both the magnitudes and the phases of these vectors.
    For example, we could represent ”prompt1” as

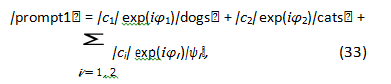
where |ci| represents the magnitude of the contribution of each basis state |ψi⟩ (e.g., ”dogs,” ”cats,” or other semantic components), and φi represents the phase. The phase information is crucial for capturing the relative relationships between different semantic components; for instance, synonyms might have similar magnitudes and similar phases, while antonyms might have similar magnitudes but opposite phases.

Illustrative Example: Semantic Clustering and Similarity To further illustrate the potential of complex embeddings, consider a simplified program that scans the alphabet to find words withclose similarity scores for words ”dog” and ”cat”. The script givesthe cosine similarity difference as

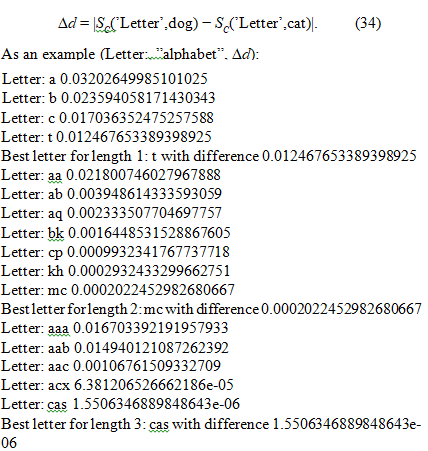
We observe that as the number of letters increases, groups of three words tend to exhibit tighter semantic clustering, with two of the words being semantically closer to the third. This increased clustering is reflected in a lower cosine similarity between the word pairs (indicating greater similarity), a trend that presumably continues with further increases in letter count. It’s also possible that longer words lead to the formation of a greater number of distinct semantic clusters, which are themselves relatively distant from each other in the overall semantic space.The program identifies ”cas” as being very similar to ”dog” and ”cat” according to some real-valued similarity metric. We might represent this in our complexified space as

This output suggests that ’cas’ and ’acx’ exhibit a high degree of similarity within the embedding space. However, cosine similarity alone fails to capture the specific differences in meaning and usage that differentiate these terms. While both might relate to the general concept of a ’situation,’ their specific connotations and contextual appropriateness may vary significantly.

In a complexified embedding space, the phase component could encode these subtle distinctions. For instance, if we consider the word ’situation’ as a superposition of basis states, the phase relationships between ’situation’ and ’cas’ might differ from those between ’situation’ and ’acx,’ reflecting their varying degrees of formality or technicality. This phase information, absent in real- valued embeddings, could provide a more refined measure of semantic similarity, enabling LLMs to generate more contextually appropriate and nuanced text.

The Mexican Hat Potential: A Geometrical Interpretation of Semantic Similarity
The cosine similarity in the real-valued embedding space can be seen as a projection of the complex similarity onto the real axis. The phase difference between two complex vectors then determines the value of the cosine similarity.

To preserve the continuous nature of the similarity measure and ensure that it remains bounded between -1 and 1, we could also consider a potential with circular symmetry in the complex plane. A potential that exhibits this symmetry is the Mexican hat potential, which allows for a continuous range of phase values while maintaining a well-defined minimum energy state, see Figure 3. The magnitude |ci| of the coefficient represents the ”distance” from the center of the hat. A larger magnitude means the state is further away from the center. Parameter φi can have values [0,2π] and it represents the angle around the circle at the bottom of the hat.

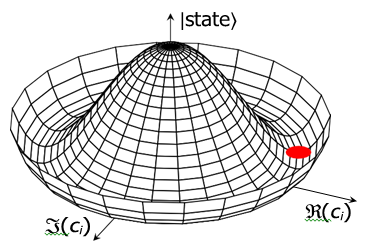
Figure 3: The Mexican hat potential, illustrating the concept of spontaneous symmetry breaking. In the context of LLMs, this potential can be used to model the emergence of stable semantic meanings, where the system ”chooses” a particular interpretation despite the potential’s inherent symmetry.
 
The Mexican hat potential is crucial in quantum mechanics and quantum field theory for illustrating spontaneous symmetry breaking, where the system selects a specific vacuum state despite the potential’s symmetry. This symmetry breaking leads to Goldstone bosons or, via the Higgs mechanism, massive gauge bosons, which are essential for understanding fundamental phenomena in particle physics, superconductivity, and cosmology.

 Semantic Wave Function: A Quantum Mechanical Formulation of Meaning

In this section, we introduce a quantum mechanical formulation of meaning within LLMs, building upon the analogy of a quantized semantic space. Our goal is to develop a tractable and interpretable model for understanding certain aspects of LLM behavior, such as
 
the superposition of semantic states and the potential for interference effects. While we acknowledge that LLMs are inherently nonlinear systems, we choose to focus on linear calculations in this section in order to simplify the mathematical analysis and to gain a more intuitive understanding of these key phenomena. We recognize that this simplification limits the scope of the model and that it may not be able to capture all aspects of LLM behavior. However, we believe that this linear formulation provides a valuable starting point for exploring the potential connections between quantum mechanics and natural language processing, and that it can serve as a foundation for future extensions that incorporate nonlinearity.
 

The foundation of our analogy lies in the observation that LLMs operate with a finite vocabulary. This means that the embedding
upon a finite set of words or tokens. We propose that each word or token in the LLM’s vocabulary corresponds to a basis state in a quantum system. We denote these basis states as |ψi⟩, where ψi represents the i-th word or token in the vocabulary. These basis states form a discrete and (ideally) complete basis for representing semantic information within the LLM. While the vocabulary is finite and therefore not truly complete in a mathematical sense, we can treat it as an approximation of a complete basis for the purposes of our analogy. The embedding vectors learned by the LLM can be seen as a representation of these basis states in a particular coordinate system. In other words, the embedding vector for a word ψi is a vector that specifies the ”direction” of the basis state |ψi⟩ in the high-dimensional embedding space
To formalize this, we define a semantic linear operator Ψ(˜ W,C), where W represents a word or phrase, and C represents the context in which it is used. We postulate that this operator acts on states

|ψi⟩ in the following way,

Ψ˜(W, C)|ψ_i⟩ = A_i(W, C)|ψ_i⟩.                                          (37)

Here, Ai(W,C) is the eigenvalue corresponding to the eigenstate |ψi⟩. This eigenvalue represents the amplitude for the word W to be associated with the semantic component represented by |ψi⟩ in the context C. The eigenstates |ψi⟩ form a complete basis for the semantic space, meaning that any semantic state can be expressed as a linear combination of these eigenstates,

where ci are complex coefficients that determine the contribution of each basis state to the overall meaning. The magnitude of ci represents the strength of that aspect of the word’s meaning in the given context, and the phase of ci encodes additional semantic information, as discussed in the previous section.

We can also express the semantic state in terms of the eigenstates of the semantic operator,

where |α⟩ is an arbitrary initial state. This equation shows how the semantic operator transforms the initial state into the semantic state |S(W,C)⟩ by weighting each eigenstate with its corresponding eigenvalue and coefficient. It is important to note that the coefficients ci are complex numbers, reflecting the extension of the embedding space to the complex domain, as discussed in the previous section. While the standard LLM embedding space is real-valued, we argue that allowing ci to be complex enables us to capture more nuanced semantic relationships and interference effects. If we are measuring the state probabilities, they are in any

Example: Probabilistic Response Generation
To illustrate this formulation, consider the following example. The system prompt is ”You are a helpful AI assistant.” The user prompt is ”””Sun is shining. It is morning. It is dark. Is the sky blue? Answer ”yes” or ”no”. Use in output only words ”yes” or ”no” ”””. We make two tests. First with the temperature = 0.9 and top p = 1.0.

The expected state is

 Semantic Distinctness: Cosine Similarity Analysis
To further illustrate the distinctness of semantic states, we perform a cosine similarity analysis on a set of related words. Using theOpenAI embeddings model, we calculate the cosine similarity between the word ”no” and several other words, including variations in capitalization and punctuation, as well as semanticallyrelated and unrelated terms. The results are as follows:

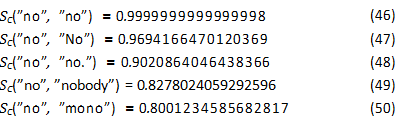
As the results demonstrate, only SC(”no”,”no”) achieves a cosine similarity of 1, indicating perfect alignment in the embedding space. All other words exhibit lower similarity scores,

case always treated as absolute values like |ci|.

highlighting their distinct semantic states. Even minor variations in capitalization or punctuation result in deviations from perfect similarity. This analysis underscores the concept that each word, even those closely related in meaning or form, occupies a unique position in the semantic space and represents a distinct basis state.

Modeling Semantic Ambiguity: The Double-Well Potential In the previous section, we introduced the concept of a semantic wave function to represent the meaning of a word or phrase in a given context. However, words often have multiple meanings, and the appropriate meaning depends on the context in which the word is used. To model this semantic ambiguity, we turn to the concept  of a double-well potential from quantum mechanics

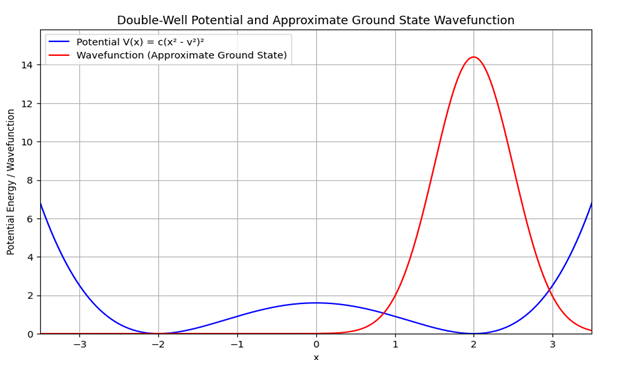
Figure 4: The double-well potential, illustrating how context can influence the interpretation of a word in LLMs. The two minima represent different meanings, and the ”tunneling” effect represents the LLM’s ability to switch between these meanings based on the surrounding context.
A double-well potential is a potential energy function with two minima separated by a barrier, see Figure 4. While not directly analogous to the Mexican hat potential discussed earlier, it provides a useful framework for understanding systems with two stable states and transitions between them. Double-well potentials appear in diverse fields like molecular physics and condensed matter, and their importance lies in illustrating fundamental concepts of symmetry breaking and quantum tunneling in a simplified, tractable system.

A typical mathematical form for a double-well potential is
V (x) = c(x² − v²)²,                                                               (51)

where c and v are positive constants. This potential has minima at
x = ±v.
The key characteristic of the double-well potential is that a particle placed in this potential will tend to settle into either minimum. Even though the potential is symmetric under reflection (x → −x), the particle ”chooses” one of the two minima, effectively breaking the symmetry. Furthermore, in quantum mechanics, a particle can tunnel through the potential barrier separating the two minima. This means that the particle can transition from one minimum to the other, even if it doesn’t have enough energy to overcome the barrier classically.

We propose that the double-well potential can be used to model semantic ambiguity in LLMs. Consider a word like ”bank,” which can refer to a financial institution or the side of a river. We can represent these two meanings as the two minima of a doublewell potential. The context in which the word ”bank” is used then determines which minimum the semantic wave function will settle into. For example, in the sentence ”The bank is open today,” the context suggests that ”bank” refers to a financial institution. The semantic wave function for ”bank” in this context, which we can denote as |S(”bank”,C1)⟩, will have a high amplitude in the minimum corresponding to the financial institution meaning. Conversely, in the sentence ”The bank of the river is eroding,” the context suggests that ”bank” refers to the side of a river. The semantic wave function for ”bank” in this context, which we can denote as |S(”bank”,C2)⟩, will have a high amplitude in the minimum corresponding to the riverbank meaning.

The ability of a particle to tunnel between the two minima in a double-well potential can be seen as analogous to the LLM’s ability to switch between different interpretations of a word or phrase depending on the context. A slight change in context can be seen as a perturbation that alters the potential landscape, causing the semantic wave function to tunnel from one minimum to the other. To illustrate this, we can consider how changes in context C affect the distribution of meanings. This is similar to how external potentials or interactions can alter the wave function in quantum mechanics. Suppose the context C changes slightly, such as by adding a new word or altering the sentence structure. This change can be represented as a perturbation â??c, leading to a change in the semantic wave function,

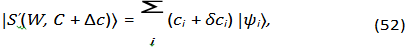
where δci represents the change in the coefficient of the basis state |ψi⟩ due to the context variation â??c.

In summary, the double-well potential provides a useful metaphor for understanding how LLMs handle semantic ambiguity. By representing different meanings of a word as different minima in a potential landscape, we can leverage the mathematical tools of quantum mechanics to analyze and understand the contextdependent nature of word meanings. The ability of the semantic wave function to tunnel between these minima reflects the LLM’s ability to switch between different interpretations based on the surrounding context.

 A Complex-Valued Similarity Measure for Semantic Representations

In previous sections, we established the framework for representing semantic information using complex-valued wave functions. This representation allows us to capture not only the magnitude but alsothe phase of each semantic component, enabling the modeling of interference effects and more nuanced semantic relationships. In this section, we introduce a new similarity measure that takes into account both the magnitudes and the phases of these complexvalued semantic representations.

Traditional cosine similarity, which operates on real-valuedvectors, only captures the angular relationship between two vectors. It disregards the phase information that is crucial for capturing semantic interference. To address this limitation, wedefine a complex-valued similarity measure that incorporates both the magnitudes and the phase differences between the complex coefficients of the semantic wave functions.

This value is relatively low, indicating that the two texts are not very similar according to this measure. This makes sense because one text expresses happiness, while the other expresses a lack of happiness. The phase of the similarity provides information about the relative orientation of the two texts in the semantic space. This example demonstrates how the complex-valued similarity measure can capture subtle semantic differences that are not captured by traditional cosine similarity. By taking into account this measure provides a more nuanced and informative way to compare semantic representations.

 Semantic Dynamics: A Path Integral Approach
In previous sections, we established a framework for representing semantic information using complex-valued wave functions and explored the concept of potential landscapes to model semantic ambiguity. To further understand the dynamics of semantic representations in LLMs, we now introduce a path integral formulation. This formalism allows us to model the evolution of the semantic wave function over time, taking into account the various factors that influence its behavior.

The path integral formulation is based on the idea that the probability amplitude for a system to evolve from an initial state to a final state is given by the sum over all possible paths connecting those two states. The generating functional is

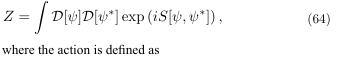
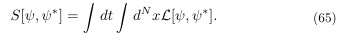
The Langrangian density L[ψ,ψ^∗] defines the dynamics of a system in N-dimensional phase. In our context, the ”system” is the semantic wave function, the ”initial state” is the initial meaning of a prompt, and the ”final state” is the LLM’s response. Our goal is to derive an ”effective” action that describes the dynamics of this semantic wave function.

 Lagrangian Density and Nonlinearity
We begin by establishing a baseline using the linear Schr¨odinger equation. While LLMs are inherently nonlinear systems due to their neural network architectures and training processes, analyzing the linear case first provides a valuable point of comparison  for understanding the effects of incorporating nonlinearity.This approach allows us to isolate and understand the specific contributions of nonlinear terms in shaping the dynamics of the semantic wave function.

To introduce nonlinearity, we consider two distinct mechanisms: (1) the addition of a cubic term to the wave equation, resulting in a nonlinear Schr¨odinger equation, and (2) the introduction of a Mexican hat potential. The nonlinear Schr¨odinger equation, characterized by a cubic term, is a common starting point for studying nonlinear quantum systems. This nonlinearity allows the semantic wave function to interact with itself. The strength and nature of this self-interaction is determined by the coupling constant, γ. A positive coupling constant (γ > 0) can be interpreted as semantic self-reinforcement, where the presence of a particular semantic meaning enhances itself. Conversely, a negative coupling constant (γ < 0) represents semantic self-inhibition, where the presence of a semantic meaning suppresses its own presence. These interpretations allow us to relate the parameter γ to the semantic coherence and diversity of
 the LLM.
The second approach to introducing nonlinearity involves the Mexican hat potential. This potential, already discussed in earlier sections, provides an alternative mechanism for capturing nonlinear effects and for the spontaneous symmetry breaking that can happen within the LLM.

Based  on  these  considerations,  we  propose  the  following Lagrangian density for the semantic wave function,when interpreting the physical meaning of the parameters. The Lagrangian LS epresents the linear Schr¨odinger equation and corresponds to the propagation of a classical free particle, while

when interpreting the physical meaning of the parameters. The Lagrangian LS epresents the linear Schr¨odinger equation and corresponds to the propagation of a classical free particle, while the term LN encompasses the nonlinear components. For the nonlinear Schr¨odinger equation, the nonlinearity has the form

 

 Introduction of Gauge Field and U(1) Symmetry
To ensure the stability of our model and prevent the arbitrary creation or destruction of semantic information, we impose a U(1) symmetry. This symmetry guarantees that the total ”semantic charge” is conserved. In quantum field theories, U(1) symmetry is associated with the conservation of electric charge, and we draw an analogy to the conservation of semantic meaning.

 

Gauge Fixing (Coulomb Gauge)
The gauge freedom in the Lagrangian leads to redundant degrees of freedom, which need to be removed to obtain a well-defined path integral. To do this, we choose the Coulomb gauge,

∂iAi = 0.              (78)

This choice simplifies calculations and has a physical interpretation in our context, as we will discuss later. To implement the Coulomb gauge, we use the Faddeev-Popov procedure. We can define number ”1”,

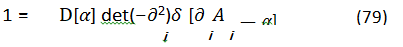
where ∂ ² is the Laplacian in N dimensions, δ is a delta function and α is some function. Then, we insert this into the path integral. We also introduce a Lagrange multiplier field λ to enforce the gauge condition. After integrating out the Lagrange multiplier, we have a generating functional,

Mean-Field Approximation
Directly integrating out the gauge fields Aµ to obtain an effective action that depends solely on ψ and ψ∗ poses significant challenges. Therefore, we implement the mean-field approximation, a common technique to simplify such calculations. This simplification, while enabling analytical progress, neglects quantum fluctuations and correlations, potentially overlooking subtle but importantaspects of the semantic dynamics. The validity of the mean-field approximation relies on the assumption that fluctuations around the mean field are small. This assumption is more likely to hold whenthe system is strongly interacting or when the number of degrees of freedom is large. In the context of LLMs, this could correspond to situations where the semantic space is highly structured or whenthe LLM has a large number of parameters.

In the mean-field approximation, we decompose the quantum fields into their average (classical) values and fluctuations around these averages. Now ψ is a complex field and needs some attention, but we may express it and the gauge field Aµ as

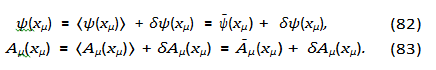
Here, ψ¯(xµ) and A¯µ(xµ) denote the mean fields, while δψ(xµ) and δAµ(xµ) represent the corresponding fluctuations. We invoke the assumption that these fluctuations are small in magnitude compared to the mean fields, which is a central tenet of the mean-field approximation. In the context of LLMs, interpreting the mean field ψ¯(xµ) as the mean field, it provides how common states happen in the embedding space.

Next, we treat the term |ψ|2 as a background ”semantic charge” density. Within this approximation, we can solve for the component A of the gauge field in terms of ψ and ψ∗. Employing the Coulomb gauge, the equation of motion for A₀ is derived by applying the Euler-Lagrange equation. Concretely, we suppose that we’re  evaluating the amount of this action with respect to a ”ground” (classical field) level of activity that measures whether or not we’ve hallucinated.
The equation of motion for A₀ is then obtained by varying the action with respect to A₀,

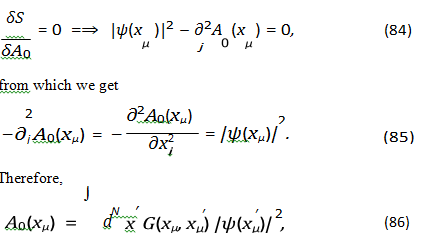
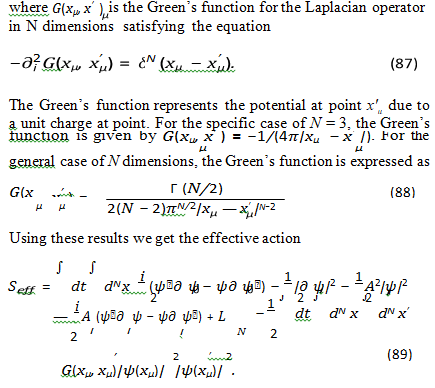
Interpretation of Terms
The effective action provides a framework for understanding how semantic meanings interact and evolve within the LLM embedding space. We can analyze the key terms in the effective action to gain insights into these dynamics. The gauge fields, particularly the vector potential Ai, play a crucial role in shaping this semantic landscape, acting as directional forces that guide the flow of semantic information. While the precise nature of these forces remains speculative, we can explore some concrete examples of how they might manifest within LLMs.

The kinetic energy term, proportional to |∂ ψ |2, relates to the smoothness or coherence of semantic meaning. A smaller gradient implies a more uniform or consistent meaning across the semantic space, while larger gradients may indicate ambiguity or rapid shifts in meaning. This term is expressed as

The term governs the temporal evolution of the semantic wave function. It dictates how the semantic meaning changes over time,with the rate of change being influenced by the other terms in theLagrangian. The gradient term for ψ, given by

penalizes rapid changes in the semantic wave function across the semantic space. This term encourages semantic smoothness and coherence. A large gradient would correspond to abrupt shifts in meaning, which are generally disfavored in coherent text generation. This term can be related to the concept of ”semantic distance” - the further apart two points are in the semantic space, the more ”costly” it is to transition between them

The interaction term between ψ and A_i is

One concrete example of how the vector potential could influence this flow is through its analogy to attention mechanisms in Transformer networks. Consider the sentence, ”The dog chased the ball, but it was too fast.” When processing ”it,” the vector potential (represented by the attention weights) would strongly connect ”it” to ”ball,” indicating that ”it” refers to the ball. This connection guides the flow of semantic information, ensuring that the LLM correctly understands the pronoun reference. Without this directional influence, the LLM might incorrectly associate ”it” with ”dog.” In this sense, the attention weights can be seen as components of the vector potential, directing the semantic current (Ji) towards the relevant parts of the input sequence. The semantic density interaction is at point xµ in the semantic space, with higher values indicating a stronger presence of that particular meaning at that location. The distance | xµ - x'µ | represents the semantic distance between points xµ and x'µ in the semantic space, with smaller distances implying a closer semantic relationship. This term suggests that words or phrases with similar semantic charges and located close to each other in the semantic space will experience an attractive or repulsive force, depending on the sign of G(xµ , x'µ). The -1/2 factor scales the magnitude of this interaction. This long-range interaction could be related to the ability of LLMs to capture dependencies between distant parts of a text, although the strength of these dependencies is now scaled down. The Green’s function G(xµ , x'µ) determines the strength and form of this interaction.

In summary, the effective action provides a rich framework for understanding the dynamics of semantic meaning in LLMs. Each term in the action corresponds to a specific aspect of semantic interaction and evolution. By analyzing these terms, we can gain insights into how LLMs process and generate language. It is important to emphasize that these interpretations are speculative, and further research is needed to validate these connections. However, they provide concrete examples of how the vector potential could play a role in guiding the flow of semantic information within LLMs.

Understanding the Cubic Nonlinearity

The cubic nonlinearity in the nonlinear Schr¨odinger equation (NLSE) introduces a term that depends on the intensity of the wave function, |ψ|². This implies that the wave function interacts with itself, and the strength and nature of this interaction are determined by the coupling constant γ. The sign and magnitude of γ significantly influence the behavior of the semantic wave function and can be interpreted in several ways.The cubic nonlinearity in the nonlinear Schr¨odinger equation (NLSE) introduces a term that depends on the intensity of the wave function, |ψ|². This implies that the wave function interacts with itself, and the strength and nature of this interaction are determined by the coupling constant γ. The sign and magnitude of γ significantly influence the behavior of the semantic wave function and can be interpreted in several ways.

If γ > 0, the nonlinearity represents semantic self-reinforcement. In this scenario, the presence of a particular semantic meaning reinforces itself, and the stronger the initial presence of a meaning, the more it tends to amplify itself. This could be analogous to priming, where a concept already activated in the LLM’s representation becomes easier to activate further. It might also relate to confirmation bias, where the LLM tends to favor interpretations consistent with its prior beliefs or knowledge, or to semantic coherence, where the LLM tries to maintain a consistent semantic representation. Mathematically, this would lead to a self- focusing effect, where the wave function tends to concentrate in regions where it is already strong.

Conversely, if γ < 0, the nonlinearity represents semantic self- inhibition. In this case, the presence of a particular semantic meaning inhibits itself, and the stronger the initial presence of a meaning, the more it tends to suppress itself. This could be analogous to attention mechanisms, where the LLM focuses its attention on the most relevant concepts and suppresses irrelevant ones, or to inhibition of return, where the LLM avoids repeating the same concepts or ideas too frequently. It could also relate to semantic diversity, where the LLM tries to explore different aspects of a topic and avoid getting stuck in a narrow focus. Mathematically, this would lead to a self-defocusing effect, where the wave function tends to spread out and avoid concentrating in any one region.

It is also possible that the sign and magnitude of γ depend on the context. In some contexts, a concept might reinforce itself (γ > 0), while in other contexts, it might inhibit itself (γ < 0). This context-dependent semantic interaction could be analogous to polysemy, where the same word can have different meanings in different contexts, or to irony and sarcasm, where the intended meaning of a statement can be the opposite of its literal meaning. It could also relate to topic shifts, where the LLM can change its focus depending on the conversation or the task. Modeling this would require a more complex model where γ is a function of the input prompt or the internal state of the LLM. The cubic nonlinearity affects the interaction between different semantic components, represented by different wave functions. To model this, one would need to consider a system of coupled NLSEs, one for each semantic component. The nonlinearity would then involve terms like |ψ |²ψ , which represent the influence of the i-th component on the j-th component. This could be analogous to semantic networks, where concepts are connected to each other in a network, and the activation of one concept can influence the activation of other concepts, or to argument structure, where the meaning of a sentence depends on the relationships between its different parts. This would lead to a much more complex model, but it could capture more nuanced semantic interactions.

In summary, the cubic nonlinearity in the NLSE model offers a way to capture interactions within the semantic space of LLMs. The specific interpretation of this nonlinearity, and particularly the sign and magnitude of the coupling constant γ, depends on the specific semantic phenomena being modeled. Further research is needed to determine the most appropriate interpretation and to develop more sophisticated models that can capture the complexities of semantic meaning and interaction.

Spontaneous Symmetry Breaking and Semantic Bias

The key difference in Mexican hat potential to the cubic nonlinearity is that the Mexican hat potential provides a mechanism for spontaneous symmetry breaking. The semantic field ψ will tend to settle into one of the minima of the potential, breaking the symmetry of the Lagrangian. This could be interpreted as the LLM ”choosing” a particular interpretation or perspective, even in the absence of specific input 

The interplay between the kinetic energy term, the Mexican hat potential, and the Coulomb interaction could lead to the emergence of complex semantic structures in the LLM embedding space. The Mexican hat potential provides a stable foundation for these structures, while the Coulomb interaction allows for long-range interactions between different semantic concepts.The spontaneous symmetry breaking inherent in the Mexican hat potential has profound implications for the interpretation of LLMs. The choice of a particular vacuum state v = |v|exp(iθ) represents a fundamental bias in the LLM’s semantic representation.

The magnitude |v| = p ²/(2λ) determines the overall strength of  this bias, while the phase θ determines the specific direction of  various ways, such as a preference for certain types of information, a tendency to adopt certain viewpoints, or a predisposition to generate certain types of text. It is important to note that this  bias is not necessarily a negative thing. It could be a reflection of the LLM’s training data or its intended purpose.  However,  it is important to be aware of this bias and to understand how it might influence the LLM’s behavior. Furthermore, the fluctuations around the vacuum state can be interpreted as the specific semantic content of the LLM’s output. These fluctuations are influenced by the input prompt, the LLM’s internal state, and the interactions between different semantic concepts.

In summary, the path integral formulation with the Mexican hat potential provides a powerful framework for understanding the dynamics of semantic meaning in LLMs. The spontaneous symmetry breaking inherent in this model leads to the emergence of a fundamental semantic bias, which influences the LLM’s behavior and shapes its output.

This section provides a detailed calculation of the effective action obtained by integrating out the vector potential Aⁱ to quadratic order, under the weak coupling approximation and in the Coulomb gauge. The weak coupling approximation assumes that the interaction between the semantic wave function and the gauge. We begin with the action that includes the vector potential Ai,

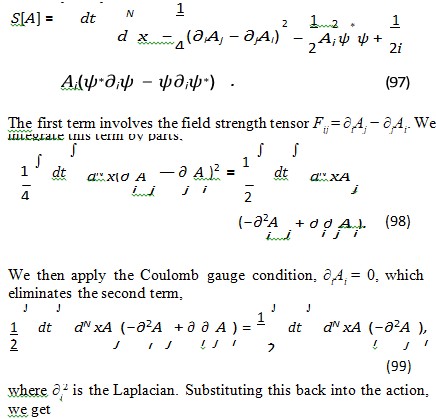
To make progress, we make the weak coupling approximation This means that we assume that the interaction between the V field and the A field is weak. This allows us to neglect the ψ*(x) ψ(xµ) term in the equation for the propagator. The validity of this approximation depends on the specific values of the parameters in the Lagrangian and the properties of the semantic wave function. In LLMs, this approximation might be reasonable if the semantic charge density is relatively low or if the gauge coupling is weak. The inverse Kernel satisfies the following equation.

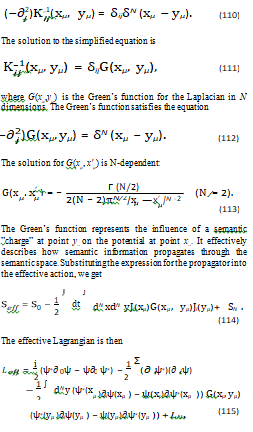
This effective Lagrangian describes the dynamics of the ψ field, taking into account the effects of the integratedout Ai field to quadratic order in the weak coupling approximation. The next to last term represents a non-local interaction between the ψ field at different points in space, mediated by the Green’s function G(xµ,yµ). This non-local interaction implies that the semantic meaning at one point in the semantic space can directly influence the semantic meaning at other points, even if they are far apart. This could be related to the ability of LLMs to capture long-range dependencies in text.

The effective action, derived from this Lagrangian, provides a powerful tool for analyzing the behavior of LLMs. By studying the solutions to the equations of motion derived from this action, we can gain insights into how LLMs process and generate language. However, it is important to remember that this model is based on several simplifying assumptions, and its predictions should be interpreted with caution. Further research is needed to validate this model and to explore its implications for our understanding of LLMs.

Interpretation of the Effective Lagrangian: Impact of Approximations
The effective Lagrangian, derived after integrating out the gauge field Ai and employing the weak coupling and mean-field approximations, provides a modified perspective on the semantic dynamics within LLMs compared to the initial Lagrangian. It is crucial to understand how these approximations influence the interpretation of the terms and the overall model. In the original Lagrangian (Equation 77), the interaction between the semantic wave function ψ and the gauge field Ai was explicit and local. Terms involving Ai directly coupled the semantic current and density to the vector potential at the same spatial point, representing a direct and immediate influence of the gauge field on the semantic wave
function.

However, the effective Lagrangian (Equation 115), obtained after integrating out Ai and applying the weak coupling approximation, exhibits a key difference: the emergence of a non-local interaction term. This term, involving the Green’s function G(x,y), couples the semantic current at point x to the semantic current at point y, integrated over the entire semantic space.This non-locality has several important implications. The original Lagrangian primarily captured local interactions. In contrast, the effective Lagrangian explicitly incorporates long-range dependencies between different regions of the semantic space. This suggests that the semantic meaning at one location can directly influence the semantic meaning at distant locations, mediated by the Green’s function. This is particularly relevant in the context of LLMs, which are known for their ability to capture long-range dependencies in  may be viewed as analogous to the self-attention mechanism in Transformer architectures [1], which enables the model to attend  to different parts of the input sequence, irrespective of their proximity.

Furthermore, the integration of Ai effectively generates an ”effective potential” governing the interaction between semantic elements. This potential is encoded in the Green’s function G(x,y), which dictates the strength and form of the interaction between points x and y. The shape of this potential is determined by the underlying Laplacian operator and the dimensionality of the semantic space. The approximations employed to derive the effective Lagrangian inevitably lead to a loss of microscopic details. By integrating out Ai, we have averaged over its fluctuations and correlations. Consequently, the effective Lagrangian only captures the average effect of the gauge field on the semantic wave function. The weak coupling approximation further simplifies the interaction, potentially neglecting higher-order effects. The mean-field approximation replaces the quantum fields with their average values, neglecting quantum fluctuations. This implies that the effective Lagrangian describes the behavior of the average semantic wave function, rather than the behavior of individual semantic elements. The validity of this approximation hinges on the assumption that fluctuations are small compared to the mean field, which may not always hold in LLMs.

In the original Lagrangian, the semantic current Ji directly interacted with the vector potential Ai, representing a local flow of semantic information. In the effective Lagrangian, the semantic current at one point influences the semantic current at another point through the Green’s function. This suggests a more distributed and interconnected flow of semantic information across the semantic space. In summary, the effective Lagrangian provides a simplified but potentially insightful framework for understanding the dynamics of semantic meaning in LLMs. The approximations made to obtain this Lagrangian introduce both advantages and limitations. The non-local interaction term captures long-range dependencies, potentially mirroring the function of self-attention, but the loss of microscopic details and the mean-field perspective limit the accuracy of the model. Despite these limitations, the effective Lagrangian offers valuable insights into how LLMs process and generate language, warranting further investigation and empirical validation.

Physical Interpretation of the Semantic Field
In the context of LLMs, our quantum-like model allows for a speculative, yet potentially insightful, interpretation of the gauge fields as representing different aspects of semantic meaning. The scalar potential, Ï? (or A0), can be interpreted as reflecting the overall semantic context or ”energy” within the LLM, influencing the probability of activating semantically aligned words. This captures the static contextual bias or ”semantic atmosphere” surrounding a word or phrase, reflecting the overall influence of the surrounding concepts. A high scalar potential might correspond to a state where the LLM is highly engaged with a particular topic, leading to a higher probability of generating words related to that topic. Conversely, a low scalar potential might indicate a state of low engagement or uncertainty. It could also bias the LLM towards certain concepts learned during training, influencing token probabilities and potentially relating to the magnitude of hidden state vectors. For example, when processing a prompt about ”climate change,” the scalar potential would be high in regions of the semantic space associated with environmental issues, scientific terms, and political debates, increasing the likelihood of generating relevant terms.

The vector potential, A, on the other hand, can be interpreted as representing the semantic relationships or ”forces” between words and phrases, guiding the flow of semantic information and shaping local interactions. This captures the dynamic flow of semantic information, reflecting shifts in topic, argument structure, and narrative flow, and possibly indicating the relationships and dependencies between different concepts. The vector potential could be related to the attention weights in Transformer networks, encoding relationships and directing the flow of semantic information. It could also encode the argument structure of verbs, specifying semantic roles, or guide topic shifts and narrative flow.

Together, Ï? and A constitute a ”semantic field” that governs the behavior of the semantic wave function, ψ. While our current model simplifies the analysis by primarily focusing on the scalar potential and often neglecting the vector potential, future research should explore the potential benefits of incorporating the vector potential to achieve a more complete nderstanding of the dynamic interplay of semantic meanings within LLMs. However, it is crucial to acknowledge the limitations of this analogy, particularly the gauge dependence of A and Ï?, and to emphasize the need for empirical validation to support these theoretical interpretations. The semantic field is likely an emergent property of the LLM’s complex neural network architecture, and its true nature remains a subject for further investigation. These interpretations are speculative, and future work should focus on developing experiments to test these hypotheses, such as analyzing attention weights or measuring the influence of perturbations on the semantic space.

Assumptions and Limitations
The quantum-like model presented in this paper relies on several simplifying assumptions, which are important to acknowledge and discuss. These assumptions allow us to develop a tractable mathematical framework, but they also introduce limitations that could affect the validity of our conclusions and the scope of our interpretations.

Completeness of Vocabulary
One key assumption is that the LLM’s finite vocabulary forms an approximately complete basis for representing semantic information. This assumption allows us to treat the semantic space as a discrete space built upon a finite set of basis states, simplifying the mathematical formalism and enabling the analogy to quantum systems with discrete energy levels. However, it is crucial to recognize that the vocabulary is not truly complete. New words and phrases are constantly being created, and the LLM’s vocabulary may not capture all of the nuances of human language, especially in specialized domains or rapidly evolving cultural contexts. Furthermore, the use of sub-word tokenization, while helpful for handling out-of-vocabulary words, can create semantic units that are not explicitly present as single entries in the vocabulary, potentially blurring the lines between discrete basis states.

This limitation could affect the model’s ability to accurately represent semantic concepts that are not wellrepresented in the vocabulary. For example, the model might struggle to understand slang terms, technical jargon, or newly coined words. It might also lead to inaccuracies when dealing with rare or specialized language, or when encountering subtle semantic distinctions that are not explicitly encoded in the vocabulary. The assumption of vocabulary completeness also neglects the dynamic nature of language, where word meanings evolve and new concepts emerge over time.

 Linearity of Operations on the Semantic Space (Given Nonlinear Training)
In several parts of our analysis, we make assumptions that implicitly treat operations on the semantic space as linear. It’s crucial to acknowledge that this is a simplification, given that the LLM’s training process is inherently nonlinear, and the resulting embedding space reflects this nonlinearity. While we perform linear operations on the learned embeddings, the embeddings themselves are the product of a highly nonlinear process. This ”inherited nonlinearity” means that our linear operations are still influenced by the underlying nonlinear structure of the embedding space, but they may not be able to fully capture its richness. These linearity assumptions manifest in several key aspects of the model:
1.    Plane Wave Approximations: The approximation of semantic waves as plane waves, solutions to linear wave equations, simplifies wave behavior and neglects potential distortions or interactions that would arise in a nonlinear medium.
2.    Superposition of Semantic States: The representation of a semantic state as a linear superposition of basis states, |α⟩
= Pci|ψ ⟩, assumes that the meaning of a complex phrase is simply the sum of the meanings of its individual components, weighted by coefficients. This neglects the possibility of emergent meanings arising from the interaction of words.
3.    Linear Schr¨odinger Equation (Initial Formulation): The initial use of the linear Schr¨odinger equation to model semantic wave propagation assumes that the semantic wave function evolves linearly, without self-interaction or interaction with other semantic components.
4.    Complex-Valued Similarity Measure: The complex-valued ∗similarity   measure, S (text1, text2) =  c c2i , calculates similarity by summing the products of complex coefficients, a linear operation. This assumes that overall similarity is a sum of component similarities, neglecting nonlinear relationships between components.
5.    The derivation of the Green’s function relies on solving a simplified, linearized differential equation (the Laplacian). This simplification arises from the combined effect of the mean-field approximation and the weak coupling approximation. The mean-field approximation linearizes the problem around the average fields, neglecting fluctuations. The weak coupling approximation further simplifies the equation by dropping terms that couple the semantic wave function and the gauge fields. While the full problem is inherently nonlinear due to terms in the Lagrangian that couple ψ and Aµ, these approximations allow us to obtain an analytic expression for the Green’s function, which would otherwise be intractable. This linearized Green’s function then describes the propagation of the average semantic potential, neglecting nonlinear effects and fluctuations.
 
The reliance on linear operations limits the model’s ability to capture complex semantic phenomena. For example, consider the sentence ”That’s sick!” In modern slang, ”sick” can mean ”amazing” or ”excellent,” a meaning that is not a linear combination of the dictionary definition of ”sick.” Similarly, the meaning of a metaphor like ”Time is a thief” cannot be derived by simply adding the meanings of ”time” and ”thief.” Irony and sarcasm also rely on nonlinear inversions of meaning. The model’s reliance on cosine similarity, a linear measure, further reinforces this limitation.

Mean-Field Approximation
When applying the path integral formalism, we employ the mean- field approximation, which assumes that the quantum fields can be approximated by their average values, neglecting quantum fluctuations. This approximation greatly simplifies the calculations and allows us to obtain an effective action that depends only on the average semantic wave function, providing a tractable framework for analyzing the dynamics of the semantic space. However, the mean-field approximation neglects important fluctuations and correlations, which could play a significant role in the dynamics of the semantic space, particularly at smaller scales or in highly dynamic contexts.

Consequently, the model’s ability to capture subtle semantic effects and emergent phenomena, such as the spontaneous emergence of new meanings or the rapid shifts in topic that can occur in natural language, could be affected. It might also lead to inaccuracies when dealing with highly dynamic or unpredictable language, where fluctuations play a more prominent role. The mean-field approximation also assumes a degree of homogeneity in the semantic space, which may not always be valid.

Weak Coupling Approximation
In deriving the effective action, we also employ the weak coupling approximation, which assumes that the interaction between the semantic wave function and the gauge field is weak. This assumption simplifies the calculation of the effective action and allows us to obtain an analytical solution, providing a more manageable mathematical framework. However, the interaction between the semantic wave function and the gauge field might be strong in some cases, particularly when dealing with highly charged or polarized semantic concepts, such as those a ssociated with strong emotions or deeply held beliefs.

This may have implications for the model’s ability to accurately capture the influence of the gauge field on the semantic wave function in these situations. It might also lead to inaccuracies when dealing with highly emotional or persuasive language, where the gauge field plays a more prominent role in shaping the semantic landscape. The weak coupling approximation also implies that the semantic charge density is relatively low, which may not always be the case in LLMs that have learned to represent complex and nuanced semantic relationships.

Static Potential Landscapes
When modeling semantic ambiguity using potential landscapes (e.g., double-well potential, Mexican hat potential), we often assume that these landscapes are static and do not change over time. This assumption simplifies the analysis and allows us to focus on the equilibrium states of the semantic wave function, providing a more tractable framework for understanding how LLMs handle multiple meanings. However, the potential landscapes are likely to be dynamic and to change over time in response to the input prompt, the LLM’s internal state, and the interactions between different semantic concepts. The context in which a word is used can significantly alter its meaning and the corresponding potential landscape.

The assumption of a static potential landscape could limit the model’s ability to capture the dynamic evolution of semantic meaning and the influence of context on word meanings. It might also lead to inaccuracies when dealing with language that is highly dependent on context or that involves rapid shifts in meaning. The assumption of static potential landscapes also neglects the learning process, where the potential landscapes themselves are shaped by the LLM’s training data.

Specific Gauge Choice (Coulomb Gauge)
In applying the path integral formalism, we have chosen the Coulomb gauge, which simplifies calculations and has a physical interpretation in terms of semantic charge conservation. However, the Coulomb gauge is not the only possible gauge choice, and other gauge choices might provide different insights into the behavior of the semantic space. The physical interpretation of the gauge fields is also gauge-dependent, meaning that the meaning we ascribe to the scalar and vector potentials depends on the gauge we choose.

The choice of the Coulomb gauge could influence the interpretation of the results and limit the generality of the model. While the Coulomb gauge provides a convenient framework for understanding semantic charge conservation, it might not be the most natural or appropriate choice for all situations. Other gauge choices might reveal different aspects of the semantic landscape and provide alternative interpretations of the gauge fields.

 Simplified Representation of LLM Architecture
It is also crucial to acknowledge that our model provides a highly simplified representation of the complex neural network architecture of LLMs. We have abstracted away many of the details of the Transformer architecture, including the multi-head attention mechanism, the feedforward networks, and the residual connections. While these simplifications allow us to develop a tractable mathematical framework, they also limit the model’s ability to capture the full complexity of LLM behavior. The model does not explicitly account for the role of different layers in the network, the flow of information between layers, or the specific activation functions used in the neurons.

The simplified nature of the model could affect the model’s ability to accurately predict the behavior of LLMs in all situations. It might also limit the model’s ability to provide insights into the specific mechanisms that drive LLM performance. The model should be seen as a high-level abstraction that captures some of the key principles underlying LLM behavior, rather than a detailed simulation.

Hallucinations and Semantic Charge Conservation: A Question for Future Investigation
This section explores a potential, albeit speculative, link between the constraints imposed by our model and the phenomenon of hallucinations in LLMs. We frame this connection as a question for future investigation, aiming to provide a new perspective on the origins of untruthful or nonsensical text generation. Within our model, the imposition of the Coulomb gauge can be interpreted as enforcing a form of semantic charge conservation. Analogous to charge conservation in electromagnetism, we hypothesize that the total semantic meaning within the LLM’s representation (represented by the integral of |ψ|2 over the semantic space) remains approximately constant. This constraint reflects the finite vocabulary and the underlying structure learned during training. The LLM, in essence, redistributes semantic meaning across its vocabulary to represent different concepts and relationships, but the total amount of meaning remains bounded. A key question arises: does the stability of this semantic charge conservation correlate with the generation of truthful and coherent text? We propose that deviations from this idealized conservation, potentially arising from noise, incomplete modeling of contextual influences, or inherent limitations in the LLM’s representation, might be indicative of, or even directly contribute to, instances of hallucination.

Several mechanisms could lead to deviations from semantic charge conservation. The LLM might fail to fully account for the context in which a word or phrase is used, leading to an inappropriate redistribution of semantic charge. For example, if the LLM misinterprets a negation, it might assign semantic charge to the wrong concept, leading to a factual error. Random noise in the LLM’s internal state could disrupt the delicate balance of semantic charge, leading to the creation of spurious meanings or the amplification of irrelevant concepts. If the LLM has overfit its training data, it might simply memorize specific facts or patterns without truly understanding the underlying semantic relationships. In this case, it might generate text that is factually correct but semantically incoherent, effectively violating semantic charge conservation. The complex, non-linear interactions within the deep neural network architecture of LLMs could lead to emergent phenomena that are not captured by our simplified model.

Alternatively, even within a system that nominally conserves semantic charge, inherent noise and fluctuations in the model’s dynamics could lead to the transient emergence of spurious or ”hallucinatory” meanings. These fluctuations could manifest as virtual particles within the semantic space, momentarily borrowing energy to create fleeting, nonsensical semantic constructs. The creation and annihilation of these virtual particles could, in effect, lead to a temporary violation of semantic charge conservation at a local level, even if the overall charge remains approximately conserved. This perspective suggests that techniques used to regularize LLMs and prevent overfitting might be seen as analogous to mechanisms that suppress the creation of virtual particles in a quantum field theory, thereby maintaining the integrity of the semantic space. These techniques effectively dampen fluctuations and encourage the LLM to learn more generalizable semantic representations. While these connections are currently speculative, they suggest that our framework offers a new perspective for investigating the relationship between model constraints, semantic stability, and the generation of truthful text.

Discussion

This paper presents a quantum-like model offering a new perspective on the inner workings of Large Language Models (LLMs). By drawing analogies to concepts from quantum mechanics, such as superposition, interference, potential landscapes, and path integrals, we have developed a framework for understanding how semantic meaning is represented and processed within these complex systems.

The application of quantum mechanical concepts to the analysis of LLM embedding spaces is a relatively unexplored area, offering the potential for new insights. The model provides intuitive explanations for several observed phenomena in LLMs, such as the probabilistic nature of their outputs, their ability to handle semantic ambiguity, and the longrange dependencies between words and phrases. The use of mathematical tools from quantum mechanics, such as the Schr¨odinger equation and the path integral formalism, provides a more rigorous framework for analyzing LLM behavior than purely descriptive approaches, potentially leading to new tools and techniques for analyzing, interpreting, and manipulating LLMs based on quantum mechanical principles.

However, it is crucial to acknowledge that LLMs, despite their impressive capabilities, remain essentially ”black boxes.” Their internal workings are complex and opaque, making it difficult to understand precisely how they process and generate language. The quantum-like model presented in this paper is not intended to be a complete or definitive explanation of LLM behavior. Rather, it is an attempt to provide a more interpretable framework for understanding their behavior, offering a new set of tools and concepts for analyzing their internal representations and dynamics. By drawing analogies to quantum mechanics, we hope to shed light on the emergent properties of LLMs and to inspire new avenues for research.

The model is based on analogies and interpretations, rather than direct empirical evidence, and it is not yet clear whether LLM embedding spaces actually behave in the way predicted. It is likely an oversimplification of the complex dynamics of semantic meaning, as many factors known to influence LLM behavior, such as the training data, the model architecture, and the specific task, are not explicitly accounted for. The physical interpretation of the vector potential A and the scalar potential Ï? in the context of LLMs requires further clarification. The use of the mean-field approximation further simplifies the model, potentially neglecting important fluctuations and correlations, and the model has not yet been rigorously tested against empirical data from LLMs.

Key results include demonstrating that the probabilistic nature of LLM outputs can be understood in terms of a quantum two- level system, arguing that extending the embedding space to the complex domain is necessary to capture semantic interference effects, developing a quantum mechanical formulation of semantic representation using a ”semantic wave function,” showing how potential landscapes can be used to model semantic ambiguity, introducing a new, complex-valued similarity measure, presenting a path integral formalism for modeling LLM behavior, discussing the implications of Coulomb gauge fixing, and speculating on the connection between deviations from semantic charge conservation and hallucinations.

Several broad research directions emerge from this work. Further investigation into the concept of semantic charge, its conservation properties, and its relationship to LLM behavior is warranted. This includes developing methods for measuring semantic charge, exploring the mechanisms that lead to deviations from conservation, and investigating the connection between semantic charge conservation and the generation of truthful and coherent text. Exploring the potential of quantum computing to enhance LLM capabilities is a promising area for future research. If the semantic space exhibits a truly quantized structure, quantum algorithms could offer advantages in tasks such as efficient semantic search, where quantum search algorithms, like Grover’s algorithm, could potentially accelerate the process of finding the closest semantic matches for a given query in the embedding space. Quantum simulation techniques could be used to model the dynamic evolution of semantic wave functions, potentially capturing emergent phenomena and subtle semantic interactions that are difficult to simulate classically. Quantum machine learning algorithms could be explored for training LLMs, potentially leading to models with improved performance, new capabilities, or more efficient training processes.

Leveraging the extensive body of knowledge surrounding path integrals in physics offers a rich set of tools for analyzing LLM dynamics. Adapting techniques from quantum field theory and high-energy physics, such as perturbation theory, renormalization group methods, and the development of Feynman diagrams, could provide new insights into the interactions between semantic concepts and the emergence of complex semantic structures. Developing ”classical LLM Feynman diagrams” to visualize and calculate effective actions could offer a powerful framework for understanding and predicting LLM behavior. In addition, insights from nonlinear optics are directly applicable to this endeavor.

We could also reconsider our approach to the inherent probabilistic behavior of LLMs. While current efforts largely focus on mitigating specific inaccuracies like ”hallucinations,” our quantum-like model suggests a broader perspective. If LLMs operate within a fundamentally probabilistic semantic space governed by quantum- like principles, then this inherent uncertainty is not merely a source of errors, but a fundamental characteristic affecting all aspects of their operation. Instead of solely trying to suppress specific manifestations of this probabilistic behavior, perhaps we can learn to harness it. Just as quantum microscopes exploit quantum fluctuations to achieve resolutions beyond classical limits, could we leverage the inherent uncertainty of LLMs to generate new ideas, explore creative possibilities, or uncover hidden relationships within data? This paradigm shift, from error correction to opportunistic exploitation of inherent probabilistic behavior, could unlock new and unexpected applications for LLMs.

References

1.    Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.

2.    J. Devlin, M-W. Chang, K. Lee, and K. Toutanova. 2018. BERT: Pre-training of deep bidirectional transformers for language understanding.

3.    Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., ... & Amodei, D. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33, 1877-1901.

4.    D. Mimno and L. Thompson. 2017. The strange geometry of skip-gram with negative sampling. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pages 2298–2307.

5.    Tenney, I., Xia, P., Chen, B., Wang, A., Poliak, A., McCoy, R. T., ... & Pavlick, E. (2019). What do you learn from context? probing for sentence structure in contextualized word representations. arXiv preprint arXiv:1905.06316.

6.    Jolliffe, I. T. (2002). Principal component analysis for special types of data (pp. 338-372). Springer New York.

7.    Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of machine learning research, 9(Nov), 2579- 2605.

8.    G. Salton and M. McGill. 1986. Introduction to Modern Information Retrieval, McGraw-Hill,

9.    Mitchell, J., & Lapata, M. (2010). Composition in distributional models of semantics. Cognitive science, 34(8), 1388-1429.

10.    Arora, S., Li, Y., Liang, Y., Ma, T., & Risteski, A. (2018). Linear algebraic structure of word senses, with applications to polysemy. Transactions of the Association for Computational Linguistics, 6, 483-495.

11.    Shannon, C. E. (1948). A mathematical theory of communication. The Bell system technical journal, 27(3), 379-423.

12.    Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM journal of research and development, 5(3), 183-191.

13.    Laine, T. A. (2023). Anomaly and Brownian fluid particle in Navier-Stokes turbulence. arXiv preprint arXiv:2310.06007.

14.    Cardy, J. (1996). Scaling and renormalization in statistical physics (Vol. 5). Cambridge university press.

15.    W. Heisenberg. 1925. Uber quantentheoretische Umdeutung kinematischer und mechaniseher Beziehungen. Zeitschrift fu¨r Physik, 33/(1):879-893.

16.    E. Schrodinger. 1926. Quantisierung als Eigenwertproblem. Annalen der Physik, 384(6):489-527.

17.    Dirac, P. A. M. (1925). The fundamental equations of quantum mechanics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 109(752), 642-653.

18.    E. Merzbacher. 1970. Quantum Mechanics, John Wiley & Sons, Singapore.

19.    Dirac, P. A. M. (1927). The quantum theory of the emission and absorption of radiation. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 114(767), 243-265.

20.    Dirac, P. A. M. (1930). A theory of electrons and protons. Proceedings of the Royal Society of London. Series A, Containing papers of a mathematical and physical character, 126(801), 360-365.

21.    P. Ramond. 1990. Field theory: A modern primer, Addison- Wesley, USA.

22.    Kaku, M. (1993). Quantum field theory: a modern introduction. Oxford university press.

23.    R. A. Bertlmann. 1996. Anomalies in Quamtum Field Theory, Clarendon Press, USA.

24.    Schwinger, J. (1948). Quantum electrodynamics. I. A covariant formulation. Physical Review, 74(10), 1439.

25.    Coleman, S. (1985). Aspects of symmetry: selected Erice lectures. Cambridge University Press.

26.    Wigner, E. (1939). On unitary representations of the inhomogeneous Lorentz group. Annals of mathematics, 40(1), 149-204.

27.    Higgs, P. W. (1964). Broken symmetries and the masses of gauge bosons. Physical review letters, 13(16), 508.

28.    Englert, F., & Brout, R. (1964). Broken symmetry and the mass of gauge vector mesons. Physical review letters, 13(9), 321.

29.    Guralnik, G. S., Hagen, C. R., & Kibble, T. W. (1964). Global conservation laws and massless particles. Physical Review Letters, 13(20), 585.

30.    P. D. Bruza, J. Busemeyer, and L. Gabora. 2009. Introduction to the Special Issue on Quantum Cognition. Journal of Mathematical Psychology, 53(5), 303-305.

31.    Busemeyer, J. R., & Bruza, P. D. (2012). Quantum models of cognition and decision. Cambridge University Press.

32.    Atmanspacher, H., & Römer, H. (2012). Order effects in sequential measurements of non-commuting psychological observables. Journal of Mathematical Psychology, 56(4), 274-280.

33.    Widdows, D., Howell, K., & Cohen, T. (2021). Should Semantic Vector Composition be Explicit? Can it be Linear?. arXiv preprint arXiv:2104.06555.