Intensity Correlation Imaging and Nonnegative Dynamic Systems

Introduction

Recent work of the present Author has succeeded in the vast reduction of integration times that have so long plagued the Hanbury Brown- Twiss effect. The way is now open to reap the advantages of simple, inexpensive flux-collecting hardware, immunity to seeing conditions, and unlimited baselines and image resolution. Furthermore, since the Brown- Twiss effect has been extended to two-dimensional imaging; it is appropriate that we term the algorithm the Intensity Correlation Imaging (ICI) algorithm. Within the mathematics featured in references [1-3] the reduction of integration times has been accomplished by means of the Noise Reducing Phase Retrieval (NRPR) algorithm which is embedded within a Stochastic Search algorithm. In the complex analysis of, initial conditions, such as small random perturbations in the pixel intensities and other complexities, the algorithm performed very well [3]. However, in this paper, we update and simplify the algorithm by constructing a discrete-time dynamic system. Moreover, not only does the algorithm perform as well as the original, but we also introduce the benefits of a nonnegative dynamic system. We progress as follows. Section 2 begins with the NRPR algorithm, which contains the correct integration times and sets up the foreground/background dichotomy. Section 3 transforms the NRPR steps into a discrete-time, nonnegative dynamic system. Section 4 merges the dynamic system within the Stochastic search algorithm structured to gradually reduce the “Box” sizes.

 Description of the NRPR Algorithm
It is supposed that there is an array of flux collecting apertures arranged so as to form a square, evenly spaced grid on the “u-v plane” (which, in interferometry, denotes the Fourier domain projected on the plane perpendicular to the target line-of-sight). The grid has a one-to-one correspondemce to a matrix of N × N pixels forming the construction of an image of a luminous object amidst a black sky. The defining characteristics of the NRPR algorithm are:

The matrix τ defines the set of constraints. τ_kj = 1 declares pixel (k, j) to be constrained to be zero, where as τ_kj = 0 if g_{k j} is unconstrained.

 
of this noise model was accomplished in resulting in an asymptotic expression for the precision estimate of the necessary integration time [1].

The second initial specification is g = g₀ where g₀ is independently and uniformly distributed in (0, δ) where δ is real and positive. It is these random specifications of the initial values of the pixel intensities that we wish to supplant with a dynamic system having additional simplifications. It must be emphasized that only a single data batch of measured coherence magnitude measurements will be used in the process by which the zero-noise image is determined. Thus the adaptive algorithms described here do not increase the necessary integration time.

However, the adaptive algorithms require repeated NRPR computations, and each such repetition uses a new seed for the randomized initial guess for the image. The various steps A to F of the algorithm are discussed in References [1-3]. The basic computations of NRPR are directed to an hypothesis that a square “box” of size Bx and, positioned in the center of the field of view, contains the noise-free image. Then NRPR is embedded within the Stochastic Search wherein the hypothesis is tested and the noise-free image is discovered.

The NRPR Algorithm as a Discrete-Time Dynamic System
As the next step in our analysis, we recast the equations of Figure 2 into a discrete-time dynamic system such that all the principal quantities are indicated by the sequence of integers k = 0, 1, ... ∞. We start with the initial conditions and the first iteration and recite the sequence of further iterations, keeping the algorithm in its proper order:

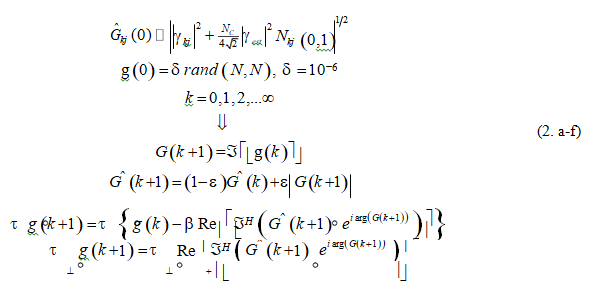
where the function rand (N, N) is an N × N matrix having statistically independent elements that are uniformly distributed in [0,1). Now consider the equations pertaining to k = 0 and 1:

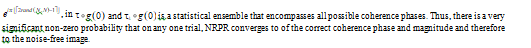
The Stochastic Search Algorithm For Sequential Box Sizes
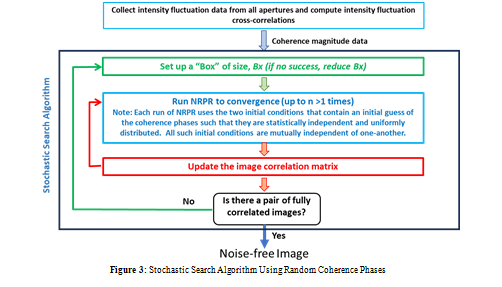
In this Section, we consider the Stochastic Search algorithm employing random coherence phases within the two initial conditions rather than random pixel intensities. Figure 3 shows that the embedded NRPR runs (in blue) use statistically independent and uniformly distributed coherence phases spanning ïÂÃÂ??ï?­ïÂÃÂ?° ,ïÂÃÂ?° ï?© . The search sets up a square “Bx” and runs NRR n > 1 times until there are two images that are fully correlated. In that case, the two outcomes are the noise-free image (baring 180 degrees of rotation or translations). If there are no such correlations within n computations, then the algorithm reduces the box size and tries again. If by chance a converged image has pixel intensities that reside outside of the box, this indicates that the box is too small to contain the illuminated object, and the box size must be enlarged. Overall this is the process by which the Stochastic Search validates the hypotheses of the box size.

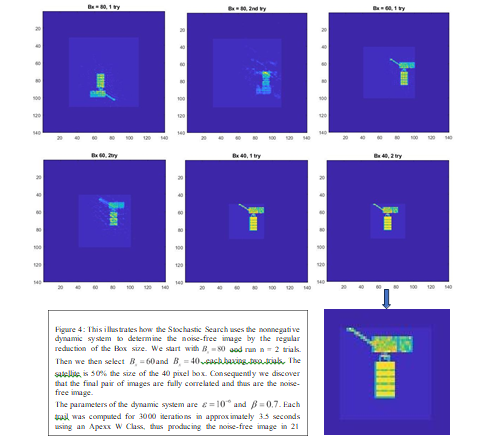
In Figure 4 we demonstrate that the dynamic system (5. a-f) behaves essentially as in References [1-3] when in the case that the smallest box size does fully contain the illuminated object. Alternately, one can start with a box size that is smaller than the illuminated object and then increase the box sizes until the noise-free image is found. With this strategy, the number of NRPR computations is distinctly reduced. In fact, if the number of runs is large for the case of decreasing box size, then for the same image, the number of runs for the case of increasing box sizes is halved. The latter strategy, As mentioned in Reference [3], the latter strategy is clearly superior.

Conclusion

Reference [1-3] created an algorithm that emphatically reduced the integration times of the Brown-Twiss effect as applied to two- dimensional imaging (termed ICI). However, there were a number of complexities in the algorithm that merited simplification. This paper has succeeded in streamlining the ICI algorithm by transforming the six steps of the original algorithm into a discrete-time, nonnegative dynamic system having a three-dimensional state space. It is demonstrated that this dynamic system fully replicates the original to within O(ε ). Furthermore, the simplified product, being a nonnegative system, is well suited to partner with Artificial Intelligence automation such as nonnegative spiking neural networks. Such automation can be expected soon [4].

Back Matter
The Author is an Independent Researcher.

Funding Sources
Aside from the Author’s efforts, there are no outside sources of funding for this Review.

Author Contributions
The Author is the sole contributor to the six journal articles under review, including the present one.

Supplementary Materials
Reside in the ICI algorithm as described in full detail within the Review.

References

1.    Hyland, D. C. (2022). Improved integration time estimates for intensity correlation imaging. Applied Optics, 61(33), 10002-10011.
2.    Hyland, D. C. (2022). Algorithm for determination of image domain constraints for intensity correlation imaging. Applied Optics, 61(35), 10425-10432.
3.    Hyland, D. C. (2023). Analysis and refinement of intensity correlation imaging. Applied Optics, 62(21), 5683-5695.
4.    Haddad, W. M., Chellaboina, V., & Hui, Q. (2010). Nonnegative and compartmental dynamical systems. Princeton University Press.