Development of a Mathematical Model of Intraoperative Balloon stretching of Soft Tissues of the Upper Limb

Introduction

A system of differential equations and regression analysis methods can be used to develop a mathematical model of intraoperative balloon sprain of the soft tissues of the hand to minimize postoperative complications and optimize the sprain process. Below is a detailed description of the model (1).

Model of Processes of Intraoperative Sprain of Soft Tissues

 Input data

t0C - initial temperature of soft tissues.
P - pressure inside the Foley catheter.
PtcO2 - partial pressure of oxygen in tissues.
t _exp - spraining time (minutes).
t _rest- rest time between sprain cycles (minutes).
T_solution - temperature of the injected saline solution.

Equations

Change in Temperature of Soft Tissue

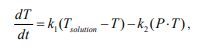
where:

T - temperature of soft tissues,

k₁ and k₂ - coefficients of heat transfer and pressure dependences

Change in Pressure in the Catheter

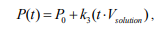
Where:
P₀ - initial pressure,
k₃ - pressure increase coefficient,
V_solutioln - volume of injected solution.

Change in Partial Pressure of Oxygen

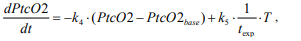
Where:

PtcO2_base - basic value of partial pressure of oxygen,

k₄ and k₅ - coefficients.

Objective Function

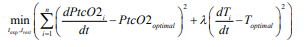
where
PtcO2_optimal - optimal partial pressure of oxygen (96.9 mmHg),
T_optimal - optimal tissue temperature (36.1°C),
λ - regularization coefficient

 Limitations
{ t exp ≤ 4   minutes
t rest ≥ 4   minutes }

Implementation

Data acquisition: Data required for each patient include initial temperature of soft tissue, intra-catheter pressure, partial pressure of oxygen, sprain and rest times.

Solving Equations

Optimization

Apply gradient descent method or other numerical methods to minimize the objective function. A program was created to solve this problem. import numpy as np from scipy.optimize import minimize.

 # Model Parameters

def model(params, T_solution, P_0, t_exp, t_rest):
k1, k2, k3, k4, k5 = params T = 36.6  # initial temperature of soft tissue
PtcO2 = 97.1 # initial partial pressure of oxygen

# Temperature Change

Function def dT_dt(T, P):=
return k1 * (T_solution - T) - k2 * (P * T)

# Pressure Change Function

def P_t(t):
return P_0 + k3 * (t * 10) # assume the volume of solution is 10 ml

 # Function for Changing the Partial Pressure of Oxygen

def dPtcO2_dt(PtcO2, T):
return -k4 * (PtcO2 - 97.1) + k5 / t_exp * T

# Integration

for
t in range(t_exp): T += dT_dt(T, P_t(t))
PtcO2 += dPtcO2_dt(PtcO2, T)

for t in range(t_rest):
T -= dT_dt(T, P_t(t))
PtcO2 - = dPtcO2_dt(PtcO2, T)
return T

# Objective Function
def objective(params):
T_solution = 42
P_0 = 320
t_exp = 4
t_rest = 4
T, PtcO2 = model(params, T_solution, P_0, t_exp, t_rest) return (PtcO2 - 96.9)**2 + (T - 36.1)**2

# Optimization

initial_params = [0.1, 0.1, 0.1, 0.1, 0.1]
result = minimize(objective, initial_params, method='BFGS'
print("optimal parameters:", result.x)

. # # Check for Adequacy

T_solution = 42
P_0 = 320
t_exp = 4 t_rest = 4
T_opt, PtcO2_opt = model(result.x, T_solution, P_0, t_exp, t_rest) print(f"Optimal temperature of soft tissue: {T_opt:.2f}°C") print(f"Optimal partial pressure of oxygen: {PtcO2_opt:.2f} mmHg.")

This model will allow us to analyze and optimize the process of intraoperative balloon sprain of the soft tissues of the hand, minimizing postoperative complications and increasing the effectiveness of the procedure [1].

The Program Will Include the Following Steps

Import of Necessary Libraries

The use of the numpy and scipy libraries for mathematical calculations and optimization. import numpy as np from scipy. optimize import minimize.

Model Definition

We will create functions to describe changes in tissue temperature, pressure in the catheter and partial pressure of oxygen.
def model(params, T_solution, P_0, t_exp, t_rest):
k1, k2, k3, k4, k5 = params T = 36.6 # initial temperature of soft tissue
PtcO2 = 97.1 # initial partial pressure of oxygen

# Temperature Change Function

def dT_dt(T, P):
return k1 * (T_solution - T) - k2 * (P * T)

# Pressure Change Function

def P_t(t): return P_0 + k3 * (t * 10) # assume the volume of the solution is10 ml

# # Function for Changing the Partial Pressure of Oxygen

def dPtcO2_dt(PtcO2, T):
return -k4 * (PtcO2 - 97.1) + k5 / t_exp * T

# Integration

for t in range(t_exp):
T += dT_dt(T, P_t(t))
PtcO2 += dPtcO2_dt(PtcO2, T)

for t in range(t_rest):
T -= dT_dt(T, P_t(t))
PtcO2 -= dPtcO2_dt(PtcO2, T)

return T, PtcO2
We determine functions that describe changes in tissue temperature, pressure in the catheter and partial pressure of oxygen. These functions use model parameters to calculate changes over time.

Definition of the Objective Function

We will create a function that will minimize deviations of temperature and partial pressure of oxygen from optimal values. def objective(params):
T_solution = 42
P_0 = 320
t_exp = 4
t_rest = 4

T, PtcO2 = model(params, T_solution, P_0, t_exp, t_rest) return (PtcO2 - 96.9)**2 + (T - 36.1)**2

The objective function calculates the deviations of temperature and partial pressure of oxygen from optimal values and sums the squares of these deviations. The optimization problem is to minimize this objective function.

Optimization of Parameters

We use the gradient descent method to find optimal values of model parameters.
initial_params = [0.1, 0.1, 0.1, 0.1, 0.1]
result = minimize(objective, initial_params, method='BFGS')
print("Optimal parameters:", result.x)

Output of Results

Output of optimal parameters and checking them for adequacy.
T_solution = 42
P_0 = 320
t_exp = 4
t_rest = 4
T_opt, PtcO2_opt = model(result.x, T_solution, P_0, t_exp, t_rest) print(f"Optimal temperature of soft tissue: {T_opt:.2f}°C") print(f"Optimal partial pressure of oxygen: {PtcO2_opt:.2f} mmHg.") [2].

After optimization, we display the found parameters and check their adequacy by calculating the values of temperature and partial pressure of oxygen at optimal parameters. This approach will allow us to optimize the process of intraoperative balloon sprain of soft tissues of the hand, minimizing the risks of postoperative complications and improving the results of the operation.

Optimal Parameters

[4.78418376e-02 -2.65076161e-04 1.40264064e-01 2.66068210e01 -1.15287207e-02] These parameters correspond to the model coefficients that were found using the gradient descent method to minimize the objective function [3].

Let us consider each of them

 k1 (4.78418376e-02)

 This parameter affects the rate of change in tissue temperature depending on the difference between the temperature of the injected solution and the current temperature of the tissue.

 k2 (-2.65076161e-04)

This coefficient affects the change in tissue temperature depending on the pressure inside the catheter. A negative value indicates that as pressure increases, tissue temperature decreases.

k3 (1.40264064e-01)

This parameter determines the rate at which the pressure inside the catheter increases during solution administration. The higher the value, the faster the pressure increase.

k4 (2.66068210e-01)

This coefficient is responsible for the rate of decrease in the partial pressure of oxygen (PtcO2) depending on the difference between the current value PtcO2 and the initial value (97.1 mmHg).

k5 (-1.15287207e-02)

This parameter affects the rate of change in partial pressure of oxygen depending on tissue temperature.

Optimal Temperatures and Partial Pressure of Oxygen

Optimal temperature of soft tissue: 36.10°C Optimal partial pressure of oxygen: 96.90 mmHg. These values were obtained by simulating the process of intraoperative sprain of soft tissues of the hand using optimized parameters.

Soft tissue Temperature (36.10°C)

The tissue temperature during sprain is maintained at 36.10°C. This value is close to normal body temperature (36.6°C), indicating that the sprain process does not cause significant overheating or hypothermia of the tissue. Maintaining the temperature within this range is important to prevent tissue damage and ensure tissue viability.

Partial Pressure of Oxygen (96.90 mmHg)

The partial pressure of oxygen in the tissues is maintained at 96.90 mmHg, which is very close to the initial value (97.1 mmHg). This indicates that the sprain process does not cause significant tissue hypoxia, which is critical for tissue state and healing after surgery. Maintaining adequate oxygen levels promotes rapid recovery and reduces the risk of postoperative complications.

The optimized parameters and the results obtained indicate that the proposed technique of intraoperative balloon sprain of the soft tissues of the hand can be successfully used to minimize the risks of postoperative complications. Maintaining temperature and partial pressure of oxygen at optimal levels promotes better tissue healing and improved functional and cosmetic results of surgery

References

1. Ahmad, H., Asghar, M. U., Asghar, M. Z., Khan, A., & Mosavi, H. (2021). A hybrid deep learning technique for personality trait classification from text. IEEE Access, 9, 146214-146232.
2. Alghazzawi, D., Bamasag, O., Ullah, H., & Asghar, M. Z. (2021). Efficient detection of DDoS attacks using a hybrid deep learning model with improved feature selection. Applied Sciences, 11(24), 11634.
3. Rashka, С. Python and machine learning [Text] / С. Rashka. – Ð?.: DMK Press, 2017. – 418 p.
4. Khattak, A., Habib, A., Asghar, M. Z., Subhan, F., Razzak, I., & Habib, A. (2021). Applying deep neural networks for user intention identification. Soft Computing, 25, 2191-2220.
5. Ziyadullaev, D., Muhamediyeva, D., Abdullaev, Z., Aynaqulov, S., & Kayumov, K. (2023). Generalized models of a production system of fuzzy conclusion. In E3S Web of Conferences (Vol. 365, p. 01019). EDP Sciences.
6. Choubey, D. K., Kumar, M., Shukla, V., Tripathi, S., & Dhandhania, V. K. (2020). Comparative analysis of classification methods with PCA and LDA for diabetes. Current diabetes reviews, 16(8), 833-850.
7. Ahmad, H., Asghar, M. U., Asghar, M. Z., Khan, A., & Mosavi, H. (2021). A hybrid deep learning technique for personality trait classification from text. IEEE Access, 9, 146214-146232.
8. Sh, Z. D., Mukhamedieva, D. T., Ziyodullaeva, G. E., & Ibadullaeva, Z. J. (2018). Develop the student model. Journal of Advanced Research in Dynamical and Control Systems– JARDCS, 10(14).
9. Ziyadullaev, D., Muhamediyeva, D., Khujamkulova, K., Abdurakhimov, D., Maksumkhanova, A., & Ziyodullaeva,G. (2024). Ensemble data mining methods for assessing soil fertility. In E3S Web of Conferences (Vol. 494, p. 02013). EDP Sciences.
10. Alghazzawi, D., Bamasag, O., Ullah, H., & Asghar, M. Z. (2021). Efficient detection of DDoS attacks using a hybrid deep learning model with improved feature selection. Applied Sciences, 11(24), 11634.
11. Mujumdar, A., & Vaidehi, V. (2019). Diabetes prediction using machine learning algorithms. Procedia Computer Science, 165, 292-299.
12. Ziyadullaev, D., Mukhamedieva, D., Teshaboyev, M., Abdurakhimov, D., Bakhodirov, M., Ziyodullaeva, G., & Abduraimov, D. (2023). Application of the neuro-fuzzy approach to solving problems of soil phases evaluation. In BIO Web of Conferences (Vol. 67, p. 02009). EDP Sciences.
13. Ziyadullaev, D., Muhamediyeva, D., Madazimov, K., Madazimov, M., Temirov, P., & Abdukadirov, D. (2024). Application of ensemble machine learning methods for diabetes diagnosis. In BIO Web of Conferences (Vol. 121, p. 01002). EDP Sciences.
14. Olimboyeva, D., Ziyadullaev, D., Mukhamedieva, D., Khujamkulova, K., Teshaboyev, M., & Ziyodullaeva, G. (2024). Solving diabetes diagnosis problems using machine learning. In BIO Web of Conferences (Vol. 121, p. 01003). EDP Sciences.
15. D.Ziyadullaev, D.Muhamediyeva, Kh.Khujamkulova, D.Ab- durakhimov, A.Maksumkhanova, G.Ziyodullaeva. Ensemble data mining methods for assessing soil fertility. E3S Web of ConferencesЭÃÂ??а ÃÂ?ÃÂ?ÃÂ??лка оÃÂ??клÃÂ??ÃÂ??ена., 2024, 494, 02013.
16. Inoyatova, M., Ziyadullaev, D., Muhamediyeva, D., Aynaqulov, S., & Ziyaeva, S. (2024). Data mining for assessing soil fertility. In E3S Web of Conferences (Vol. 494, p. 02012). EDP Sciences.
17. Avalos, M., Hellard, P., & Chatard, J. C. (2003). Modeling the training-performance relationship using a mixed model in elite swimmers. Medicine and science in sports and exercise, 35(5), 838.
18. Khattak, A., Habib, A., Asghar, M. Z., Subhan, F., Razzak, I., & Habib, A. (2021). Applying deep neural networks for user intention identification. Soft Computing, 25, 2191-2220.