A New Theoretical System Combinating Classical Mechanics and Quantum Mechanics

Introduction

Can quantum mechanics and classical mechanics be compatible? This is a fascinating question. We can be certain that many people hope the answer is yes and are interested in the results of others' strong exploration of this issue. We believe that this compatibility has a certain theoretical basis and strive to find or establish such a foundation. The Ehrenfest theorem proves that “taking the classical limit, the laws of quantum mechanics will be simplified into the laws of classical mechanics” [1,2]. This allows wave dynamics to be used to describe macroscopic objects under certain conditions in principle. When the scale of quantum systems becomes very large or quantum effects become less apparent, the description of quantum mechanics approaches the results of classical mechanics. This is the characteristic of quantum decoherence. Although there is no macroscopic object in the object it describes, there are manifestations (features) that contain macroscopic objects. If the two different behaviors of particles before and after quantum decoherence are determined by their composition, structure, and external conditions, then the two extreme cases of Ehrenfest's theorem or the starting and ending points of the quantum decoherence process are related. This connection is also the connection between classical states and quantum states. The compatibility between quantum mechanics and classical mechanics has a structural foundation. Previously, people used two methods (and the ideas and concepts determined by them) to sever this connection: the changes in microscopic particles did not conform to the law of causality; The process of quantum decoherence and other microscopic changes is an instantaneous process, and there is no causal relationship between them. It is not difficult to see that this "disconnection operation" is artificial or subjective. The deeper you delve, the less reliable you feel. The Einstein theorem can indicate that the described object is not limited by mass when using de Broglie waves. This happens to be useful for the theme of this article.

I firmly believe that all natural things are real things, and they only have real manifestations. The functions and characteristics that only gods or ghosts possess are not manifestations of real things. I believe that the correct theory is often a simple and clear theory. I believe in intuition and heartfelt thoughts. Often holding onto ideas that have spontaneously formed without external influence. I started self-learning quantum mechanics and relativity theory in 1981. The primitive ideas in the heart reject the explanation system of quantum mechanics. Therefore, while studying, strive to find the composition and structure of localized realism and determinism of atoms and molecules. We should have looked for other models only when we couldn't find locally stable hydrogen molecular ions! Therefore, I am eager to know if a localized and definite framework of hydrogen molecular ions can exist stably. According to classical electromagnetic theory, a stable hydrogen molecule ion must have a structure with one electron in the middle and two hydrogen nuclei on either side (and the middle electron must have the function of an elastic ring). This structural skeleton is like the wheels of a unicycle. Through calculations, it was found that such a structure can reach classical mechanical equilibrium. The quantitative calculation results of bond length and dissociation energy do not contradict experimental facts. I have no reason to deny the microstructure of this localized realism. The quantum mechanics method can only consider the thermodynamic stability of the system and cannot consider the dynamic stability, which makes people feel uneasy psychologically. Under this ideological concept, I continuously researched and invented a quantum chemistry method that combines quantum mechanics and classical mechanics, and proposed the theory of wave element material structure. Finally, the Schrödinger equation was established to describe the Earth's revolution - a combination of macroscopic and microscopic theories.

The Schrödinger equation of gravitational potential energy that I established myself is introduced in references [3-6]. This equation itself uses quantum mechanics methods to describe classical systems, and is the bridge between quantum mechanics and classical mechanics. It can be said that local real quantum mechanics requires such equations. This equation also requires support from the application results of local realism quantum mechanics. In references, the introduction of this equation is relatively rough [3-6]. This article will review the establishment process of the equation and provide a detailed introduction to its application scope, theoretical basis, application examples, and practical significance. The Schrödinger equation for the Earth's revolution also refers to this new equation. Sometimes it is also called the "Schrödinger equation for macroscopic objects" or the Schrödinger equation for classical systems (or the Schrödinger equation for local realism). For convenience, we refer to this type
of equation as the "Schrödinger-Tu equation".

I have made gratifying progress in establishing local realism quantum mechanics [7-11]. I found that this research work lacks some things that I am currently unclear about in theory. After establishing the Schrödinger equation that can describe macroscopic objects, I knew that this equation was one of the things I lacked.
The biggest feature of the objective of this study is the ability to simultaneously use wave mechanics and classical mechanics to  describe microsystems, Recognize and apply the compatibility of wave mechanics and classical mechanics in terms of conceptualand logical thinking [7-11]. The newly established gravitational
potential Schrödinger equation and the original Schrödinger equation may form a system of Schrödinger equations. Under appropriate conditions, entities as small as elementary particles and as large as planets (objects of local and non local realism) can be described using this system of equations. The theoretical system of local realism (including conceptual system, explanatory system, and mathematical formal system) is relatively complete. However, prior to references, theories that are compatible with non local realism still cannot be used to describe macroscopic systems [3-6]. Classical theories cannot be used to describe microscopic systems. It was only after the establishment of the Schrödinger equation for gravitational potential energy in references and this article that the theoretical system of local real quantity mechanics was further improved, which put an end to this situation [3-6]. That is to say, the macroscopic Schrödinger equation is an important component of the theoretical system of local realism quantum mechanics (after establishing the macroscopic or gravitational potential Schrödinger equation, we can intuitively see this). This article introduces the theoretical basis (background), application achievements, and significance of the macroscopic Schrödinger equation.

 Establishment of the Schrödinger Equation for Gravitational Potential Energy

One of the Schrödinger equations for Earth's rotation established in references is [3-6]

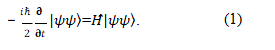
Below we will briefly introduce how equation (1) was obtained. The existing theory of quantum mechanics holds that the de Broglie waves of physical particles are complete waves (i.e., if physical particles are viewed as waves, their particle characteristics and energy are not considered). According to this understanding, the phase velocity of de Broglie waves is

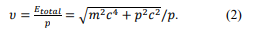
However, in wave theory, the relationship between phase velocity and frequency is

V=λv       (3)

The two methods of representing the phase velocity of de Broglie waves are inconsistent. Only one of them is factual. We believe that de Broglie waves are more similar to moving spring oscillators or vibrating strings. The fluctuation energy of a moving spring oscillator or vibrating string does not include the internal energy m_oc2 of the spring oscillator or string. The wave energy of de Broglie waves does not include the internal energy of particles, but only the kinetic energy of particles. The fact that the wave energy of the de Broglie wave is zero and its kinetic energy is also zero after the particle is stationary indicates that the wave energy of this de Broglie wave does not include the internal energy m_oc².

                V=E_k/P               (4)

In this case, the fluctuation energy hν of the de Broglie wave is Ed. By substituting hν = Ek = (1/2)mυ2 and p = mυ into equation (4), we can obtain

hν_d=(1/2)mυ².                    (5)

We are certain that the de Broglie waves of electrons are not the noumenon of wave functions (waves of wave functions). This can be seen from the statement 'when the particle is stationary, the wave function is still, while the de Broglie wave has disappeared' (and also, the wave velocities of the two waves are different). According to references [3,8], we know that, for the nounenon of wave functions ave fun E = 1/2 hvwave function, If we want to establish a connection between the wave energy of the de Broglie wave of electrons and the energy of the electron wave function, we must be electrons and the energy of the electron wave function, we must be able to use the relationship  hν_d = 2â??v_{wave function}. In this way, we can use equation (6).

Among them, ψ is usually referred to as the wave function. The use of this function and the Schrödinger equation is considered one of the proofs using quantum mechanics. The reason is that macroscopic objects in motion can also be regarded as de Broglie waves; Many people believe that the wave function is a tool, and that there is no real ontology of the wave function (using the same wave function for different particles and objects seems to be a hint). Equation (1) can also be written in the following form:

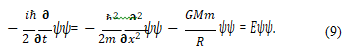
Conclusion: The standard orbital motion of the Earth conforms to equation (9).In the Eq.(9), the first term from the left of the equation is written in the form of the first derivative of the wave function with respect  to time (i.e., written as 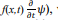 which was Schrödinger's initial choice. I will continue to use this option. The specific form of f(x,t) ∂/∂ Ψ The above equation is a time dependent Schrödinger equation. It is obtained by replacing the electromagnetic potential energy func- tion in the original Schrödinger equation 

Discussion on the Noumenon of Wave Functions
The existing theories of quantum mechanics and material structure cannot explain the source of electron spin magnetic moment. It cannot be answered what kind of intrinsic composition structure and motion lead to the wave particle duality of microscopic particles? What is the relationship between kinetic energy and E in the wave function? Is a moving elementary particle also a wave packet composed of multiple waves of different wavelengths? Is the interference of waves in the same material flow wave packet interference? Or monochromatic wave interference? If readers believe it is monochromatic wave interference (because interference between wave packets cannot be completed), will the intensity of the interference still match the observed facts? The wave packet will collapse when it encounters the instrument. Why can diffraction still occur after the wave packet collapses when the elementary particle flow passes through a slit? Is the frequency of de Broglie waves on Earth determined by its actual vibrations? Does an Earth have many vibrations that make up an Earth wave packet? For the sake of convenience, we refer to these questions as a set of unsolved mysteries concerning the structure and properties of matter. Once any of these questions are clarified, it will definitely lead to a breakthrough in theoretical research in physics.
Reference provides research materials on non-point electronic structure models [12]. The world-renowned authors in the data have completed multiple papers in the context of determinism and realism. On the basis of their research work, the authors of this article further assume that the electronic ring is not a solid ring,
but a wave ring [3,7-10].

Reference proposed a wave element material structure theory [3,7-10]. That is, assuming that electrons are localized entities composed of waves. The composition method is that the wave propagates along a very small circle, and the center of gravity of the entity enclosed by the wave can be stationary while the wave is in motion. For convenience, we refer to it as Hypothesis 1. This model effectively explains the source of electron spin magnetic moment. Under this assumption, a planetary hydrogen atom model can be constructed to smoothly explain why the energy calculated results of Bohr hydrogen atoms are very close to the facts. Under this "deterministic" material structure framework, this calculation method can be extended to diatomic small molecules such as hydrogen molecular ions and hydrogen molecules. The calculation method is simple, but the results are close to the experimental values [7-10]. In the context of assumption 1, an electron is a small charged wave ring that can expand according to Huygens' principle and form a hydrogen atom with a proton. Such hydrogen atoms are particles with planetary structures. The approach of local realism is clearly the theoretical basis for directly describing macroscopic objects using quantum mechanics methods. The theory of wave element material structure and the macroscopic object Schrödinger equation are mutually necessary and mutually confirmed. Because the macroscopic Schrödinger equation is an equation that can describe the "object of local realism".

We use the new term 'noumenon of wave function', which refers to the waves of the wave function. At present, we know very little about the noumenon (ontology) of wave functions and the essence of de Broglie waves, which leaves us with enormous space for exploration and imagination. In this way, the relationship between the noumenon of the wave function and some physical quantities in the de Broglie wave (such as the relationship between the Ewave function and the Ed, etc.) can be boldly selected based on some clues. For the relationship between the physical quantities of macroscopic and microscopic entities (such as kinetic energy, velocity, etc.) and the energy, velocity, wavelength, frequency, and momentum of the body of de Broglie waves and/or the noumenon of wave function, in addition to the agreed upon de Broglie relationships and derived relationships, we can also make the following definitions.

As long as we choose that the relationship between the wave energy and frequency of the de Broglie wave is also hν, and then according to λ = h/(mυ), we can obtain the wave energy of the de Broglie wave Ed = hν = mυ2. In references, the author points out that one of the wave of the wave function is essentially circularly polarized light, and its energy frequency relationship is E = (1/2)hν [7,9]. This provides a more in-depth explanation of the differences between waves of wave functions and de Broglie waves. The equation represents that the de Broglie wave of a moving object with non-zero stationary mass is a "kinetic wave", and the internalenergy of the object (corresponding to the stationary mass of the object, m_oc2) does not belong to the wave energy component of its de Broglie wave. When a non-zero stationary mass object is in motion, its de Broglie waves resemble a moving spring harmonic oscillator (or water waves or vibrations propagating on strings or upwards). By doing so, we can solve the problem of de Broglie phase velocities exceeding the speed of light without using the concept of group velocity.

 Examples of Using both Classical Mechanics and Quantum Mechanics Simultaneously
The research results introduced in the previous two sections have shown that classical mechanics and quantum mechanics are compatible. This section uses examples to illustrate how this compatibility can be demonstrated in applications.

If we use a planetary model, we can fully describe the hydrogen atom using the one-dimensional Schrödinger equation (which is qualitatively a combination of classical mechanics and quantum mechanics). The calculated result is also consistent with Bohr's calculation result at that time. If only this is the case, it cannot demonstrate the advantage of combining classical mechanics with quantum mechanics. However, when it comes to calculating hydrogen molecules, the advantages are very obvious (the method advantage is that it can greatly simplify the calculation process, and the theoretical advantage is that it can change human scientific concepts and promote scientific development). Please refer to references 5-11 for detailed calculation process. Here, we will only provide a brief introduction. Using local realism and determinism, as well as classical electrodynamics models or planetary models, the skeleton of hydrogen molecules is shown in Figure 1. The two electrons in the hydrogen molecule have already paired to form a two electron elastic ring. It is located between two hydrogen nuclei.

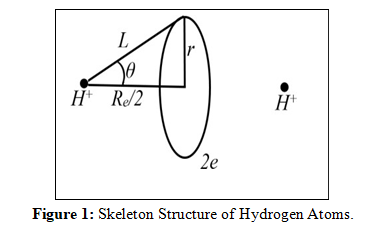
 In such a structure, the classical electrodynamic interaction equation is

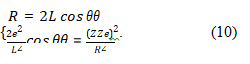
This equation has a real number solution, indicating that the hydrogen molecule structure can reach classical electrodynamic equilibrium. Solving this equation yields:

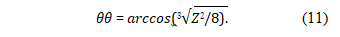
When Z = 1, θ = 60° Based on this skeletal structure, it is relatively easy to write an accurate potential energy function for hydrogen atoms. The specific calculation work has been detailed in reference [3]. The calculated results are consistent with the experimental detection values. References provide more examples [8-11]..

 The Current Interpretation System of Quantum Mechanics Is Unsatisfactory
The existing quantum mechanics is not without any problems [8,14- 16]. This clearly leaves us with space for research and exploration. It reminds us that the existing theory of quantum mechanics cannot be used as an absolute criterion for judgment. Non local realism and local realism should be allowed to coexist and complement each other. For problems that cannot be perfectly solved by the ideas and methods of local realism, use the original Schrödinger equation and the ideas and methods of non local realism to solve them. For example, the quantization and electron spin problems, as well as the fine structure problems of hydrogen atoms that cannot be solved by planetary models, can be solved using the original Schrödinger equation and non local realism methods. It is not convenient to solve the rigorous logical calculation problem of hydrogen molecules using pure quantum mechanics methods. Therefore, a planetary model is used to solve the structural problem of hydrogen molecules and improve the accuracy of the potential energy function. Assuming that the two s-electrons of a helium atom are completely overlapping 'double electrons'. Calculate the energy of this pair of electrons using quantum mechanics methods, then use a prepared regression equation to determine the interaction energy between the electrons, and finally sum them up [13]. We can obtain the energy data of helium atoms.

The interpretation system of quantum mechanics violates principles. More than 100 years have passed, but there are still many people who are not satisfied with it. Einstein is one of them [13]. He has a famous saying, 'God never rolls dice.' Recently, the journal Nature published a cover article titled ‘Why Even Physicists Still Don't Understand Quantum Theory 100 Years on’ [16]. The most important point it points out is that quantum mechanics depicts a counter-intuitive reality in which the act of observation influences what is observed — and few can agree on what that means. These situations are the breeding ground for our different perspectives.

The situations introduced in the previous sections indicate that the Schrödinger equation, which can describe the gravitational potential energy of the Earth's revolution, is not an isolated matter. The three aspects of the Schrödinger Tu equation, the new theory of wave element material structure, and the application examples of the combination of quantum mechanics and classical mechanics mutually confirm and support each other. And it can become the main content of the theoretical foundation of local realism quantum mechanics. This is our confidence in breaking through the limitations of quantum field theory and standard model theory.

Conclusion

The Schrödinger equation of gravitational potential energy itself is a product of the combination of quantum mechanics and classical mechanics, serving as a bridge between them. The Schrödinger equation and the wave function it uses belong to the category of quantum mechanics, and using the Schrödinger equation of gravitational potential energy to describe microscopic and macroscopic objects belongs to the "quantum classical mechanics" method. The establishment of the Schrödinger equation for gravitational potential energy proves that the compatibility between classical mechanics and wave mechanics has a theoretical basis. This indicates that there is no insurmountable deep trench between classical mechanics and quantum mechanics. To create a method that combines classical theory and quantum theory in the context of this research, it is necessary to first break the old views of the opposition between classical mechanics and quantum mechanics and the determination of quantum properties of microscopic particles that do not need to be considered. The various physical quantities of macroscopic objects (such as momentum, energy, wavelength, frequency, velocity, wave function, etc.) and the quantum properties of microscopic particles all originate from composition, structure, and motion. The mass of the described object is no longer an important factor in choosing which method to use (classical mechanics or quantum mechanics). The ontology of the wave function is not the same as the de Broglie wave, and treating them as the same wave is incorrect. The existing interpretation system of quantum mechanics has been strongly challenged. The comprehensive introduction of this article indicates that the Schrödinger equation of gravitational potential energy, the theory of wave element matter structure, and the calculation method of "classical mechanics and quantum mechanics can be used together for both microscopic and macroscopic objects" are not single isolated events, but complement each other and can form a new system (i.e., they are components of a new system). This new system is expected to become the foundation for new physics theories, including local realism quantum mechanics and non-point elementary particle structure theory. Starting from the theory of spacetime and mathematical methods, despite persisting for many years, there has been little progress in solving the crisis in physics. This article proposes a new path - starting from the exploration of material structure to solve the current crisis in physics.

References

1.    Richard Fitzpatrick. (2022). Ehrenfest theorem-Physics, Libre Texts. 360 library.

2.    Ehrenfest, P. (1927). Bemerkung über die angenäherte Gültigkeit der klassischen Mechanik innerhalb der Quantenmechanik. Zeitschrift für physik, 45(7), 455-457.

3.    Tu, R. (2024). A review of research achievements and their applications on the essence of electron spin. Advances in Theoretical & Computational Physics, 7(4), 01-19.

4.    Tu, R. (2024). Establishing the Schrödinger Equation for Macroscopic Objects and Changing Human Scientific Concepts. Advances in Theoretical & Computational Physics, 7(4), 01-03.

5.    Tu, R. (2025). Research Progress on the Schrödinger Equation of Gravitational Potential Energy. Adv. Theo. Comp. Phy, 8(1), 01-07.

6.    Tu, R. (2025). Research Progress on the Schrödinger Equation that Can Describe the Earth's Revolution and its Applications. London Journal of Research in Science: Natural & Formal, 25(1), 27-38.

7.    Tu, R. (2024). Solving the problem of source of electron spin magnetic moment. Physical Science International Journal, 28(6), 105-110.

8.    Tu, R. (2018). Quantum Mechanics’ Return to Local Realism. Cambridge Scholars Publishing.

9.    Tu, R. (2024). A Wave-Based Model of Electron Spin: Bridging Classical and Quantum Perspectives on Magnetic Moment. Adv. Theo. Comp. Phy, 7(4), 01-10.

10.    Tu, R. (2024). Progress and Review of Applied Research on New Theory of Electronic Composition and Structure. Infinite Energy, 28(167).

11.    Tu, R. (2014). Some Success Applications for Local-Realism Quantum Mechanics: Nature of Covalent-Bond Revealed and Quantitative Analysis of Mechanical Equilibrium for Several Molecules. Journal of modern physics, 5(6), 309-318.

 12.    Oliver Consa. (2025). Newletter#4, Top Ten influential papers.

13.    Tu, R. (2016). Principle and application of experimental method for measuring the interaction energy of electrons in atoms (Vol. 2, No. 8, pp. 187-200). International Academic Research Report.

14.    Tu, R. (2019). If the wave function collapse absolutely in the interaction, how can the weird nature of particles are born in the interaction: A Discussion on Quantum Entanglement Experiments. Indian Journal of Science and Technology, 12(8), 1-10.

15.    Einstein,  A.,  Podolsky,  B.,  &  Rosen,  N.  (1935). EinsteinPodolskyRosen. Phys. Rev., 47, 777.

16.    Carroll, S. (2025). Why even physicists still don't understand quantum theory 100 years on. Nature, 638(8049), 31-34.